Tangens kąta ostrego zaq: Równoległobok ma boki długości 2√2 i 4, a jego krótsza wysokość ma długość 2. Oblicz tangens kąta ostrego w tym równoległoboku.

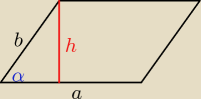
Ajtek: a=4 b=2√2 h=2 0<α<90 tgα=?

	h
sinα=		⇒ sinα=...
	b

sin^α+cos²α=1 ⇒ cosα=...

	sinα
tgα=
	cosα

I koniec.

zaq: nie mieliśmy jeszcze sinusów i cosinusów. tylko tangens. jakiś inny sposób?

Ajtek: Z tw Pitagorasa: Rysunek nie chce mi się załadować, odcinek od wysokości (czerwona), do wierzchołka kąta α oznaczam jako x: x²+h²=b² x=√b²−h²

	h
tgα=
	x