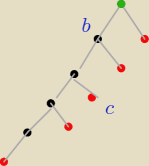
prawdopodobieństwo Krzychu: W pudełku znajduje się n kul białych (b) i jedna czerwona (c). Z pudełka losujemy po jednej kuli tak długo aż zostanie wylosowana kula czerwona. Graf obok ilustruje wyniki tego doświadczenia. a) ile kul było w pudełku przed przystąpieniem? b) określ przestrzeń zdarzeń elementarnych tego doświadczenia poprzez wypisanie jej elementów. a) to 5, ale wg mnie sie nie da określić, bo jakby czerwona wypadła za 2 razem to już powód do tego żeby mówić że było tak tylko 2 kule? b) Ω={b,bb,bbb,bbbb,bbbbc}?

Basia: ad.a nie masz racji; gdyby ich było więcej niż 5 to ostatnie pokazane losowanie też miałoby dwa możliwe wyniki z grafu wynika, że po wylosowaniu 4 kul białych została w pudełku już tylko kula czerwona ad.b Ω = {(x₁,x₂,....,x_k): k≤n i x_k=c i x₁=x₂=...=x_k−1=b}

Krzychu: a) skąd wiesz że po wylosowaniu 4 białych została juz tylko jedna czerwona? Może tam jest jeszcze kilka białych ale akurat wypadła czerwona. To jest przeciez możliwe.

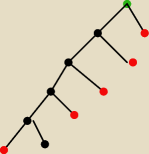
Basia: gdyby zostało jeszcze kilka białych to graf musiałby wyglądać tak jak na rysunku brak drugiej możliwości oznacza, że już nie ma białych kul

Krzychu: ok a) już czaje, ale b) nie potrafie odczytać tego co napisałaś, jestem po jednej lekcji

Basia: ta Ω ma być ogólnie czy dla n=5 ?

Krzychu: dla n=5

Basia: dla n=5 Ω = {(c); (bc); (bbc); (bbbc); (bbbbc)}

Krzychu: dlaczego to c na poczatku? przecież one nie padło samo, tylko dopiero po bbbb

Krzychu: ?