przebieg zmiennosci funkcji
qew: jezeli dziedzine funkcji mam (−2,2] to jak licze granice na końcach przedziału określoności to
tylko w −2 lewostronna i prawostronna?
a co z asymptotami?
11 gru 20:34
qew: 
?
11 gru 20:39
zośka: w −2 prawostronną, a w 2 lewostronną
11 gru 20:45
qew: ,ale w −2 trzeba również lewostronną?
11 gru 21:14
qew:
11 gru 21:30
qew:
11 gru 22:12
aniabb: w −2 prawostronną, a 2 po prostu wstawiasz
11 gru 22:13
qew: no tak,a jeśli chodzi o asymptoty pionowe,to odrazu moge określić,że bedzie to −2 tylko,że mi
wychodzi,że będzie to obustronna
11 gru 22:22
PW: Kurde, jeżeli dziedzina jest (−2,2], to którędy chcesz się skradać do −2 z lewej strony?
11 gru 22:35
qew: no tak,wiem.Nie pomyślałem.A jeśli chodzi o 2 to nie jest asymptotą?
11 gru 22:39
Mila:
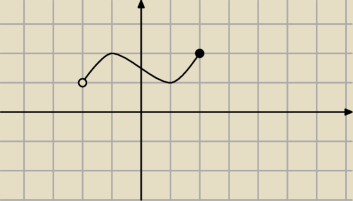
Podaj wzór tej funkcji, bo to jest rozmowa jak ze ślepym o kolorach.
Taka dziedzina nic nie mówi o asymptotach.
Przyklad.
11 gru 22:46
11 gru 22:58
Mila: f(x)=(x√(2−x)/(x+2)
D: x∊(−2;2> policzyłeś(?)
Miejsca zerowe:
x=0 oraz x=2
x=granice na krańcach dziedziny
limx→2−(x√(2−x)/(x+2)=0
limx→−2+(x√(2−x)/(x+2)=[−2*√c+/0+]=−∞ (stała dodatnia przez o+ dąży do +∞)
Asymptota pionowa x=−2
Monotoniczność:
Obliczyłeś pochodną? ?
11 gru 23:29
qew: tak obliczyłem,określiłem ich monotoniczność tylko strasznie dużo roboty z nimi było
11 gru 23:44
11 gru 23:46
qew: dziedzina to na pewno zbiór liczb rzeczywistych
11 gru 23:48
qew: funkcja nie jest ani nieparzysta ani parzysta
11 gru 23:50
qew: a jak obliczyć granice na końcach przedziału określoności czyli w −∞ oraz w∞?
12 gru 00:04
Basia:
no przecież D = (−2;2] to jakim cudem x może dążyć do + lub − ∞ ?
12 gru 00:06
Basia: chyba, że o inną funkcję Ci chodzi ?
12 gru 00:07
qew: chodzi mi o funkcje którą napisałem o 23:46
12 gru 00:18
Mila:
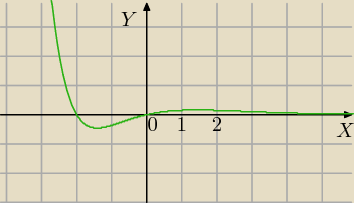
D=R
| | x*(x+2) | |
limx→∞ |
| =0 (hospital) |
| | ex+2 | |
Monotoniczność
| | x*(x+2) | | −x2+2 | |
f '(x)=( |
| )'= |
| |
| | ex+2 | | ex+2 | |
−x
2+2=0⇔x=
√2 lubx=−
√2 ( tu mogą być ekstrema)
−x
2+2>0⇔(2−
√2)(2+
√2)>0⇔
x∊(−
√2;
√2) pochodna zmienia znak w −
√2 z ujemnej na dodatnią
w x=−
√2 jest minimum lokalne y≈−0,5.. oblicz
w x=
√2 jest maksimum lokalne y≈0,16
12 gru 00:22
Basia:
no to masz
lim
x→ −∞ f(x) = lim
x→ −∞ x(x+2)*e
−(x+2) = (−
∞)*(−
∞)*(+
∞) = +
∞
| | x2+2x | |
limx→ +∞ f(x) = limx→ +∞ |
| = reguła de l'Hospitala |
| | ex+2 | |
| | 2x+2 | |
limx→ +∞ |
| = reguła de l'Hospitala |
| | ex+2 | |
12 gru 00:23
rafał: a czemu w −
∞ nie korzystałaś z hospitala
12 gru 00:30
qew: bo ex dążace do −∞ dązy do 0,wiec powstanie symbol nieoznaczony
12 gru 00:35
qew: dziękuje Basiu
12 gru 00:35
Basia:
[P⇒rafał]] bo mi nie był do niczego potrzebny
tam nie pojawia się żaden symbol nieoznaczony
12 gru 00:37
Mila: No to widzę, że niepotrzebnie pisałam.
12 gru 00:39
qew: Przepraszam Mila,również bardzo Ci dziękuje bardzo mi pomogłaś
12 gru 00:41
qew: tzn chodziło mi Basiu,że gdyby liczyć limes x→∞tak jak limes przy x→−∞ to otrzymalibyśmy
(−∞)*(−∞)*0,a ∞*0 jest to symbol nieoznaczony
12 gru 00:44
Basia: zgadza się
12 gru 00:50
qew: powiedz mi jeszcze odnośnie asymptot.pionowych funkcja nie posiada bo jest ciągła w całym
zbiorze tzn jej dziedzina to R tak?
jesli chodzi o ukośną to a=0,wiec b=0 więc asymptota pozioma to y=0(liczyłem to z limes x→+∞)
a jeśli drugi przypadek to nie ma sensu go liczyć bo a wyjdzie mi ∞ ,a musi wyjść jakaś
konkretna liczba,tak?(bo z tego wnioskuje,że ta asymptota gdzieś jest ,ale w ∞)
12 gru 00:56
Basia: zgadza się; asymptot pionowych nie ma
y = 0 jest asymptotą poziomą prawostronną
lewostronnej poziomej nie ma
ukośnej lewostronnej też nie ma bo
| | f(x) | | x+2 | |
limx→ −∞ |
| = limx→ −∞ |
| = |
| | x | | ex+2 | |
lim
x→ −∞ (x+2)e
−(x+2) = (−
∞)*(+
∞) = −
∞
a tak jak piszesz ta granica musiałaby być jakąś liczbą skończoną
12 gru 01:02
qew: a co z pkt przegięcia
12 gru 01:10
qew: druga pochodna wyszła mi x2−2x+2 przez e(x+2) zgadza się z wolphramem
12 gru 01:11
qew: wtedy gdy licznik =0?
12 gru 01:12
Basia: no to ja się nie zgadzam z wolframem
| | (2x+2)*ex+2 − ex+2*(x2+2x) | |
f'(x) = |
| = |
| | (ex+2)2 | |
| ex+2*(2x+2−x2−2x) | |
| = |
| (ex+2)2 | |
| | −2x*ex+2 − ex+2*(2−x2) | |
f"(x) = |
| = |
| | (ex+2)2 | |
f"(x) = 0 ⇔ x
2−2x−2 = 0
Δ=4+8 = 12
√Δ = 2
√3
x
2 = 1+
√3
i w obu tych punktach druga pochodna zmienia znak
czyli masz dwa punkty przegięcia
dla x∊(−
∞; 1−
√3) f"(x)>0 ⇒ f jest wypukła
dla x∊(1−
√3;1+
√3) f"(x)<0 ⇒ f jest wklęsła
dla x∊(1+
√3;+
∞) f"(x)>0 ⇒ f jest wypukła
12 gru 01:23
qew: wolfram miał dobrze,i ja też tylko żle przepisałem.Dziękuje Ci Basiu i Dobranoc
12 gru 01:32