punkty Zadanie: Zbadaj czy punkty A=(−4,−6) b=(−1,2) c=(5,6) są współliniowe

PW: Trzeba policzyć odległości między tymi punktami. Suma dwóch z nich musi być równa trzeciej.

Ajtek: Albo sprawdzić, czy leżą na jednej prostej.

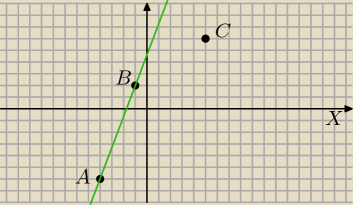
Mila: Z rysunku widać, że nie. prosta AB: 2=−a+b −6=−4a+b odejmuję stronami 8=3a

	8
a=
	3

	8		2
2=−		+b⇔b=4
	3		3

Prosta AB:

	8		2
y=		x+4
	3		3

	8		2		40		14		54
C=(5;6) spr y=		*5+4		=		x+		=		≠6
	3		3		3		3		3

Punkty nie są współliniowe

Stępień:

	8
Prosta AB: y = a1x + b1, a1 =
	3

	12
Prosta Ac: y = a2x + b2, a2 =		≠ a1, punkty A, B, C nie są współliniowe
	10

Gustlik: A=(−4,−6) b=(−1,2) c=(5,6) Wektorami:

	8
AB→=[−1−(−4), 2−(−6)]=[3, 8] ⇒a1=
	3

	12		4
AC→=[5−(−4), 6−(−6)]=[9, 12] ⇒a2=		=
	9		3

a₂≠a₁ − współczynniki kierunkowe AB i AC są różne, punkty nie są współliniowe.

Mila: I tak, masz kilka sposobów. Wybór należy do Ciebie. Polecam, abyś skorzystał też ze sposobu PW, przećwiczysz Tw. Pitagorasa.