pomocy
Lizzie: Dobrze
? Znajdź najmniejszą i największą wartość funkcji f(x)= (x−1)
2*
√x2 −2x +3
x∊<0,3)
| | 3x2 − 6x + 7 | |
f`(x) = (x−1)[ |
| ] |
| | √x2 − 2x +3 | |
WK; f`(x) = 0 ⇒ x=1
WW; f`(x) > 0 ⇒ x∊(1,3)
f`(x) < 0 ⇒ x∊<0, 1)
f(1) = 0 MIN
f(0) =
√3
f(4) = 4
√6 MAX
11 gru 16:22
Lizzie: sprawdzi ktoś?
11 gru 16:45
konrad: ok
11 gru 16:46
konrad: przy czym ten przedział miał być chyba domknięty z prawej strony
11 gru 16:48
konrad: no i ten max to dla f(3)
11 gru 16:48
Lizzie: właśnie on nie jest domknięty . x∊<0,3)
11 gru 16:52
Lizzie: tak tam ma byc f(3) a nie f(4) pomyliłam się.
11 gru 16:53
konrad: o, to jak nie domknięty to nie wiem co w takiej sytuacji...
chyba że da się jakoś policzyć wartość funkcji dla x=2,(9)
11 gru 16:55
b.:
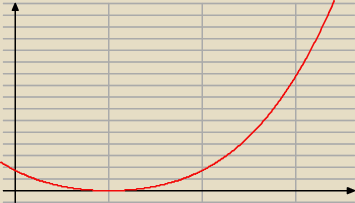
skoro przedział jest otwarty, to maksymalnej wartości nie ma...
11 gru 16:56
konrad: a nie, przecież 2,(9)=3....
to ja nie wiem
11 gru 16:56