Oblicz granicę ciągu Kamil: a_n=^{(2n−3) 2} _n+1

Artur_z_miasta_Neptuna: zapisz to jeszcze raz ale uzywając U zamiast u do zapisu ułamka

Kamil:

	(2n−3)2
an=
	n+1

Kamil: dlaczego cały czas wychodzi mi 4, a powinno być w wyniku coś innego

Artur_z_miasta_Neptuna: granica ciagu jest +∞

camus:

4n2−6n+9		6   3   n2(4− + )   n   n2
	=		=
n+1		1   n(1+ )   n

	6   3   n(4− + )   n   n2
		−> ∞
	1   1+   n

Kamil: Bardzo dziękuję

Kamil:

	2x
oblicz granicę lewostronną funkcji f(x)=		w punkcie x=1
	x−1

Artur_z_miasta_Neptuna: i w czym problem

Kamil: problem, że nie kumam tych granic

Kamil: proszę o pomoc

camus: Wskazówka: Narysuj sobię wykres tejże funkcji i zobacz gdzie zmierza y po lewej stronie asymptoty.

Kamil: czy dobrze odczyruję, że do −nieskończoności

Ajtek:

	2x
Dla x→1− x−1 dąży do 0 po liczbach ujemnych, zatem limx→∞		=−∞, ponieważ:
	x−1

2*1
	=2*(−∞}=−∞
1   −   ∞

Cześć Artur .

Kamil: dziękuję bardzo, chyba zaczynam kum kuk kum...

Mila:

	2x		2
lim x→1− (		)→		=−∞ ( podstawiasz sobie np.x=0,999999)
	x−1		0−

Ajtek: Hej Mila

Mila: Witam Cię Ajtek.

Kamil: mam jeszcze jedno pytanie do tego zadania, czy ta funkcja ma asymptotę ukośną, jeżeli tak to jakie jest jej równanie?

Artur_z_miasta_Neptuna: raczej posiada poziomą i pionową ... (pozioma to szczególny przypadek ukośnej)

Kamil: mogę prosić troszkę jaśniej

Kamil: czy dobrze myślę, że nie ma tej asymptoty

Kamil: proszę jeszcze o pomoc,

	x2
wyznacz pochodną funkcji f(x)=
	x+1

Ajtek: Ukośnej asymptoty nie ma, masz rację. Asymptota pozioma jest szczególnym przypadkiem asymptoty ukośnej, o czym wspomniał Artur. Wzór asymptoty ukośnej to y=ax+b, pozioma jest ⇔ gdy a=0 i ma wzór y=b

Ajtek:

	f		f'*g−f*g'
Wzorek (		)'=
	g		g2

Mila:

	2x
1) wykres funkcji f(x)=		masz narysowany 13:04
	x−1

jedną asymptotę zaznaczyłam: x=1 pionowa druga:

	2x		2(x−1)+2
f(x)=		=
	x−1		x−1

	2
f(x)=2+		postać kanoniczna funkcji homograficznej
	x−1

y=2 asymptota pozioma

	x2
2) y=
	x+1

[x=−1 asymptota pionowa , inne trzeba policzyć] pochodna:

	x2		2x(x+1)−x2*1		x2+2x
(		)'=		=		=
	x+1		(x+1)2		(x+1)2

	x(x+2)
=
	(x+1)2

Kamil: Witam, i dziękuję za wczorajszą pomoc. Mam problem z wyznaczeniem miejsca zerowego i znaku pochodnej funkcji

	1
f(x)=		x3−x2−3x+2
	3

Kamil: proszę o pomoc

Artur_z_miasta_Neptuna: na pewno nie pokręciles czegoś miejsc zerowych z takiego wyrażenia nie wyliczysz

Kamil: takie właśnie mam zadanie i nie wiem jak to zrobić

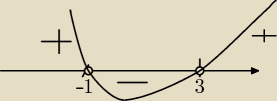
Mila: Chyba chodzi o miejsca zerowe pochodnej. f '(x)=x²−2x−3 Δ=4+12=16

	2−4		2+4
x1=		=−1 lub x2=		=3
	2		2

f '(x)>0⇔(x+1)(x−3)>0⇔ x<−1 lub x>3 funkcja dla tych argumentów jest rosnąca f '(x)<0 ⇔x∊(−1;3) funkcja malejąca

Kamil: Bardzo dziękuję za pomoc, mam coś jeszcze. Pochodna pewnej funkcji jest równa y'=e^2x(x²−1). Czy funkcja ma eksterma lokalne?

Artur_z_miasta_Neptuna: przyrównaj pochodną do 0 ... zrób szkic wykresy tejże pochodnej ... na jej podstawie oceń czy funkcja posiada ekstrema czy też nie