pochodna nina78: wyznacz zbiór wartości funkcji o tej własności, że dla dowolnej wartości parametru m styczna do jej wykresu w punkcie o odciętej m ma równanie 2m+1)x−y−m²=0 dajcie jakieś wskazówki

Nienor: To znaczy, że f'(m)=2m+1, czyli f'(x)=2x+1, ∫(2x+1)dx=x²+x+C=f(x), gdzi C jest jakąś liczbą w ℛ.

nina78: a nie używając całek

nina78: alo jeszcze raz proszę o pomoc

MQ: Równanie stycznej dla x=m (2m+1)x−y−m²=0 czyli: y=(2m+1)x−m² ale ponieważ jest to dla x=m, więc punkt styczności ma współrzędne: x=m y=(2m+1)*m−m²=m²+m Ale punkt styczności należy do wykresu funkcji, więc wykres funkcji jest zbiorem: {(x,y): x=m, y=m²+m} Stąd wynika, że poszukiwana funkcja ma postać: y=x²+x No i teraz wyznacz sobie zbiór jej wartości.

nina78: dziękuj baaaaaaaaaaaaaaardzo a takie: dla jakich wartości parametru m zbiór rozwiązań x²+(m+3)x+m≤−2 zawiera się w przedziale [−1,3] co w tych warunkach jest źle 1' Δ=0 −1≤Xw≤3 2' Δ>0 f(−1)≤0 f(3)≤0

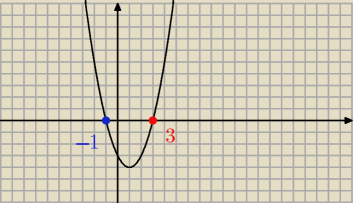
Nienor: x²+(m+3)x+m+2≤0, dla x∊[−1,3] czyli (x+1)(x−3)=x²+(m+3)x+m+2 x²−2x−3=x²+(m+3)x+m+2 −2=m+3 ⇒ m=−5 Strasznie to proste, tam u góry pochodne, tu na dole takie.