Ciągi zombi: Udowodnij, że jeżeli 3 kolejne kąty czworokąta wpisanego w koło tworzą ciąg arytmetyczny, to co najmniej dwa kąty tego czworokąta są proste.

⎧	α+a1+r=180o
⎩	a1+2r+a1=180o

⇒ α=a₁+r oraz wiem, że są to kąty, które lezą naprzeciw siebie, czyli α+α=180^o ⇒ α=90^o i a₁+r=90^o Wystarczy coś takiego?

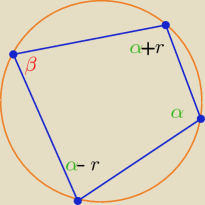
Eta: Z treści zadania: (α−r)+(α+r)= 180^o i α+β= 180^o 2α=180^o ⇒ α= 90^o i β= 180^o−α= 90^o Mamy już dwa kąty proste, jeżeli r= 0 to i dwa pozostałe (α−r) i (α+r) też będą proste czyli co najmniej dwa kąty są proste c.n.u