planimetria
Olka: Podstawa trójkąta równoramiennego ma długosć 4 a ramiona 8:
a) oblicz dłuogść promienia wpisanego w trójkąt.
b) oblicz dłuogść promienia opisanego na trjkcie
27 maj 18:01
Marek: długość promienia wpisanego to:
r = 2Pa+b+c gdzie P to pole tego trójkąta
promień opisany to
R = a*b*c4*P gdzie P to pole tego trójkąta
P = 12 a * h
h2 + (12a)2 = b2
h2 + 22 = 82
h2 = 64 − 4
h2 = 60
h = 2√15
P = 12 * 4 * 2√15
P = 4√15
27 maj 18:12
Marek: oczywiście u Ciebie a = 4 b=c=8
27 maj 18:13
osoba z 3 z matmy :P:
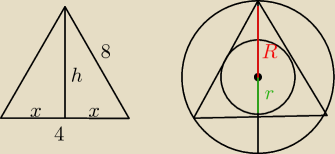
Tak więc do tego zadania potrzebne nam są założenia, że:
Promień okręgu wpisanego w trójkąt r=
13h
Promień okręgu opisanego na trójkącie R=
23h
Tak więc:
Potrzebujemy h, które możemy obliczyć dzięki pitagorasowi

a więc:
2x=4
x=2 cm
x
2 + h
2 = 8^
h
2 = 8
− 2^
h
2 = 64 − 4
h =
√60
h ≈ 7,75 cm
i teraz zaczynamy podpunkty:
a)
r=
13h
r=
137,75 cm
r ≈ 2,58 cm
b)
R=
23h
R=
237,75 cm
R ≈ 5,16 cm
27 maj 18:25
kate : no pierwsza osoba dobrze kombinowała, zmaczy się z dobrych wzorów .
oo ; )
27 maj 21:22
kate : a druda osoba pomyliła ; p
bo to są wzory na długości promieni w trójkącie równobocznym

ale no, z całym szacunkiem 3 z matmy sie nalezy za kombinowanie ; )
27 maj 21:23
Olka: Czyli dobrze mi wyszło

dzięki
27 maj 21:59
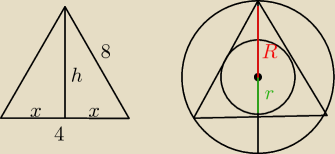 Tak więc do tego zadania potrzebne nam są założenia, że:
Promień okręgu wpisanego w trójkąt r=13h
Promień okręgu opisanego na trójkącie R=23h
Tak więc:
Potrzebujemy h, które możemy obliczyć dzięki pitagorasowi
Tak więc do tego zadania potrzebne nam są założenia, że:
Promień okręgu wpisanego w trójkąt r=13h
Promień okręgu opisanego na trójkącie R=23h
Tak więc:
Potrzebujemy h, które możemy obliczyć dzięki pitagorasowi  a więc:
2x=4
x=2 cm
x2 + h2 = 8^
h2 = 8 − 2^
h2 = 64 − 4
h = √60
h ≈ 7,75 cm
i teraz zaczynamy podpunkty:
a)
r=13h
r=137,75 cm
r ≈ 2,58 cm
b)
R=23h
R=237,75 cm
R ≈ 5,16 cm
a więc:
2x=4
x=2 cm
x2 + h2 = 8^
h2 = 8 − 2^
h2 = 64 − 4
h = √60
h ≈ 7,75 cm
i teraz zaczynamy podpunkty:
a)
r=13h
r=137,75 cm
r ≈ 2,58 cm
b)
R=23h
R=237,75 cm
R ≈ 5,16 cm
 ale no, z całym szacunkiem 3 z matmy sie nalezy za kombinowanie ; )
ale no, z całym szacunkiem 3 z matmy sie nalezy za kombinowanie ; )
 dzięki
dzięki