rozwiąż równanie grappiso: 4sin³x − 8sin²x − sinx + 2 = 0

aniabb: sinx=t t∊<−1;1> 4t³−8t²−t+2 = 0 4t²(t−2) −1(t−2) = 0 (4t²−1)(t−2)=0 (2t−1)(2t+1)(t−2)=0 t=1/2 t=−1/2 t=2 odrzucamy sinx=1/2 lub sinx=−1/2 x=30° +k*360 lub x=150° +k*360 lub x=210° +k*360 lub x=330° +k*360

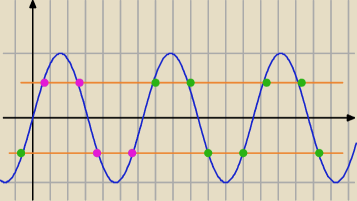
aniabb: te 4 iksy to rózowe a te k*360 to zielone

grappiso: ogromne dzięki!

grappiso: Mogłabyś mi jeszcze tylko pomóc z: 2sin⁵x − 3sin³x +sinx = 0 ? Wystarczyłby tylko sposób na skrócenie tego równania

aniabb: sinx=t t(2t⁴−3t²+1) = 0 w nawiasie t² = m 2m²−3m+1 delta i odstawiasz do t

grappiso: dzięki, bardzo mi to pomogło!