Boki trójkąta ABC zawierają się w prostych o równaniach...
Ayami: Boki trójkąta ABC zawierają się w prostych o równaniach:
y = −5/3x + 25/3
y = −3x + 3
y = −5x + 15.
Wyznacz:
a) równania prostych zawierających środkowe tego trójkąta
b) współrzędne punktu przecięcia środkowych trójkąta ABC.
9 gru 23:04
aniabb:
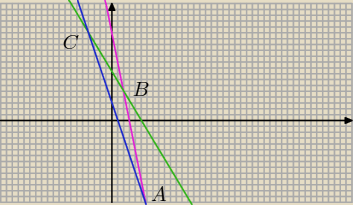
aby A
y=−3x+3
y=−5x+15
A(6;−15)
aby B
y=−5/3x+25/3
y=−5x+15
B(2;5)
aby C
y=−3x+3
y=−5/3x+25/3
C(−4;15)
9 gru 23:27
aniabb: środek AC to D(1,0)
środkowa BD to y=5x−5
środek AB to E(4,−5)
środkowa CE to y=−2,5x+5
środek BC to F(−1;10)
środkowa AF to y=25/7 x +45/7
9 gru 23:34
aniabb: przecinają się środkowe
y=5x−5
y=−2,5x+5
podstawiając
7,5x=10
więc
x= 4/3
y=5/3
9 gru 23:36
baca:
| | 6 + 2 − 4 | | −15 + 5 + 15 | | 4 | | 5 | |
Środkowe przecinają się w punkcie ( |
| ; |
| ) = ( |
| ; |
| ) |
| | 3 | | 3 | | 3 | | 3 | |
9 gru 23:44