pochodna 2: Mam takie zadanie, oblicz pochodną:

	2sin2 x
y=
	3cos2 x

No to korzystam z wzoru na iloraz i funkcję złożoną: y'=2^{sin2 x}*ln2*2sinx*cosx*3^{cos2 x} − 3^{cos2 x}*ln3*2cosx*(−sinx)*2^{sin2 x}

	1
*		Rozwala się edytor więc zapisałem tak.
	32cos2 x

Dalej w liczniku upraszczam wyłączając przed nawias 2^{sin2 x}*2sinx*cosx*3^{cos2 x}(ln2+ln3)=2^{sin2 x}*sin2x*3^{cos2 x}ln6 Więc całość:

2sin2 x*sin2x*3cos2 xln6
32cos2 x

A odpowiedź

ln6*6sin2 x*sin2x
	i nie wiem jak to się wzięło.
3

2:

Mila: To jest to samo, tylko inna postać: rozpiszę Ci potęgi:

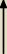
2sin2x * 31−sin2x
	=
32−2sinx

	2sin2x *3 *3−sin2x
=		= odejmujemy wykladniki przy potęgach o
	32*3−2sin2x

jednakowych podstawach

	2sin2x*3sin2x
=		= mnożymy podstawy, bo wykładniki są jednakowe.
	3

	6sin2x
=
	3