zad
Mat: Określ, w zależności od wartości parametru m, liczbę pierwiastków równania I x2 − 2x | =m
należących do przedziału <−2,2>.
9 gru 15:29
krystek: Napisałam Tobie .
9 gru 16:06
Mat: Wykres prosty , ale mam odpowiedz do zadania i dla mnie jest jakaś dziwna , no i nie wiem...że
niby liczbe rozwiazan generuja liczby 1 i 8 nie wiem jakim cudem/// ....
9 gru 16:09
Eta:
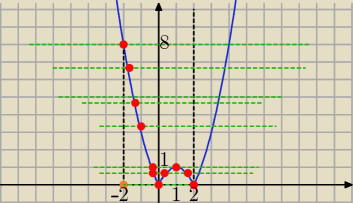
dla m<0 0 rozwiązań
dla m €(1,8> 1 rozwiązanie
dla m= 1 i m=0 2 rozwiązania
dla m€ (0, 1) 3 rozwiazania
9 gru 16:10
Eta:
f(−2)= |4+4|= 8
9 gru 16:12
Mat: możesz to wytłumaczyć ? kompletną niewiedze mam , wykres taki ale skąd odpowiedź ...
9 gru 16:13
Mat: Kurde wiem już...
9 gru 16:14
Mat: tyle że w tej odpowiedzi jest jeszcze ze 8,+oo − brak rozwiazan ...
9 gru 16:14
Eta:
Zielone proste g= m przecinają ten niebieski wykres w przedziale <−2,2>
widzisz ile razy? ( czyli tyle rozwiązań w tym przedziale dla odpowiednich 'm"
9 gru 16:15
Mila:
| | 2 | |
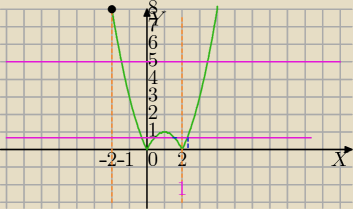
wsp. wierzchołka parboli xw= |
| =1 |
| | 2 | |
y
w=|1−2|=1
f(−2)=|4−2*(−2)|=8
f(2)=0
1) m<0 brak pierwiastków
2) m=0 dwa pierwiastki ( x=0, x=2)
3) m∊(0;1) są 4 pierwiastki, ale tylko 3 należą do przedziału <−2;2>
4)m=1 są 2 pierwiastki należące do przedziału <−2;2>
dokończ
9 gru 16:15
Eta:
No tak
0 rozwiązań jeszcze powyżej 8 czyli dla m€ (8,
∞) ( dopisz jeszcze ten przedział
bo te rozwiązania będą już poza przedziałem <−2, 2>
Jasne?
9 gru 16:17
Eta:
9 gru 16:18
Mat: Wszystko jasne, dziękuję bardzo
dasz radę zrobić jeszcze jedno zad z funkcji ?
9 gru 16:19
Eta:
@
Mila ....... gdzie widzisz te 4 rozwiązania?
9 gru 16:20
krystek: Oj Eto trudne zadanie stawia przed Tobą Mati.\Eto przeczytaj moją uwagę w poprzednim poście
Matiego.
9 gru 16:21
Mat: 2x3−(3m−1)x2+7x−m=0 , pierwiastkiem rownania jest −1 , wyznacz m i pozostałe pierwiastki ...
9 gru 16:21
Mat: hahha i nie żaden Mati krystek
9 gru 16:22
Eta:
Wiem, czytałam
9 gru 16:22
Eta:
@
Mat
W(−1)=0 i jazda wyznacz "m"
przy wyznaczonym "m" podziel W(x) : ( x+1)
otrzymasz równanie kwadratowe i dalej już z górki i bingo
9 gru 16:24
krystek: Wyznacz m z warunku W(−1)=0
9 gru 16:25
Mat: Ale banał hahaha !
jestem dziewczyną i nie chce mi sie zmieniac tego Mat
to jeszcze jedno , wykaż że
x
4−2x
3+2x
2−6x+9 nie ma pierwiastkow rzeczywistych ...
9 gru 16:27
Eta:
x4−2x3+x2 +
x2−6x+9=0
a z tego:
(x
2−x)
2 + (x−3)
2≠0 ( podaj komentarz dlaczego ?
9 gru 16:31
Mat: Albo coś lepszego :
x
2+px+p=0 ma dwa różne pierwiastki. Za pomoca wzorow Vieta zbadaj czy istnieje p, przy ktorym
(x
1 + 2x
2) (x
2 + 2x
1) osiaga wartosc 1
9 gru 16:32
Mat: Jejku nie zadawaj mi takich trudnych ...
no bo są kwadraty tak ? czy coś takiego (?)
9 gru 16:35
Mat: Pomożecie ?
9 gru 16:43
Mat: Eta, krystek Help ! Jest tam ktoś jeszcze ?
9 gru 16:50
Eta:
| | 1 | |
taka wartość istnieje dla p= |
| |
| | 2 | |
9 gru 16:53
Mat: a może tak jakieś obliczenia ?
9 gru 16:56
Mat: dacie radę wyprowadzić wzór na sume odwrotnosci pierwiastkow kwadratow z Vieta ?
ważne !
9 gru 16:57
Mat: Czy to by bylo (b2−2ac)/ c2 ?
9 gru 16:58
Eta:
1/ Δ>0 ⇒ p
2−4p>0 ⇒ p€ ............
2/ x
1+x
2=−p i p≠0 (bo x
2=0 to x=0 −−− odpada
x
1*x
2=p
W= x
1*x
2+2x
12+2x
22+4x
1*x
2= 2(x
12+x
22)+5x
1*x
2=
= 2[(x
1+x
2)
2−2x
1*x
2]+5x
1*x
2= 2(x
1+x
2)
2+x
1*x
2
to W=1 ⇒ 2(−p)
2+p=1 ⇒ 2p
2+p−1=0 ⇒ (2p−1)(p+1)=0
dokończ ....... uwzględnij Δ>0
i zjedz koniecznie dobre
(zapobiega sklerozie ... matematycznej też
9 gru 17:05
Eta:
| 1 | | 1 | | b2−2ac | |
| + |
| = ... = |
| |
| x12 | | x22 | | c2 | |
9 gru 17:08
Mat: Danke! ja nie mam czasu jeść przez te matme... null ... eh dzięki że poświęciłaś swój czas...
mogę napisać jeszcze jakieś jesli chciałabyś ?
9 gru 17:10
Mat: Eta czy Ty się nie pomyliłaś .... ?
9 gru 17:12
Mat: taka wartość istnieje dla p=1/2 a przecież ono nie należy do dziedziny
9 gru 17:12
Mat: wychodzi na to że p= −1 , a to p=1/2 odrzucamy bo z delty wychodza p e −oo,0 i 4,+oo
9 gru 17:14
Mat: 2p2+p−1=0 to z tego −1/2 nie wyjdzie...
9 gru 17:29
Eta:
taaaak p=−1
( domownicy mi przeszkadzali , bo chcieli jeść
9 gru 17:30
Mat: o kurde , masz możliwość usuwania ? O.O dobra dzięki Ci bardzo , namęczyłyśmy się , daję Ci
spokoj juz dziś
9 gru 17:32
Eta:
9 gru 17:33
Mat: Dzięki jeszcze raz
9 gru 17:34
krystek: Eta Czarodziejka!
9 gru 17:34
Mat: owszem
a krystek leń , tylko podgląda !
9 gru 17:36
krystek: Napracowałam się i odpoczywam. Pomoc domowa ma dużo pracy przed świętami mimo niedzieli.
9 gru 17:37
Mat: Dobrze,bo niedziela to dzien roboczy mimo wszystko
9 gru 17:39