Wyznacz dziedzinę funkcji
matema: Wyznacz dziedzinę funkcji:
| | 2−x | |
c) f(x)=√x2+3x+2+ln( |
| ) |
| | x | |
9 gru 14:43
9 gru 14:47
matema: | | 2−x | |
a nie powinno być |
| ≥0  |
| | x | |
9 gru 14:50
matema: bo przecież x w mianowniku powinien być różny od 0
9 gru 14:51
9 gru 14:53
ICSP: poczytaj o dziedzinie logarytmu to Ci się rozjaśni,.
9 gru 14:53
asdf: matema, znajdz mi logarytm z zera, albo inaczej:
3x = 0
rozwiąż
9 gru 14:54
ICSP: a ja mogę to rozwiązać czy ten przykład tylko dla matematmy ?
9 gru 14:55
matema: nie da się rozwiązać
9 gru 14:56
matema: ICSP pomóż

9 gru 14:57
krystek: logab zał a>0 i a≠1 i b>0
9 gru 14:58
ICSP: dobra
jednak 3
x = 0 nie posiada rozwiązań

Głupi przykład

9 gru 14:58
matema:
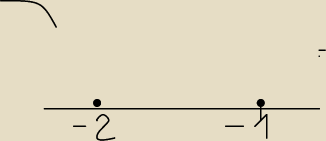
moje rozwiązanie
x
2+3x−2≥0
Δ=1
x
1=−2 x
2=−1
x∊(−
∞;−2>u<−1;−
∞)
9 gru 15:02
matema:

2−x>0 x<0
9 gru 15:04
matema: na wykresie po kolei −2, −1, 0, 2
9 gru 15:04
matema: i odpowiedź x∊(−∞;−2>u<−1;−∞)
9 gru 15:05
9 gru 15:05
matema: napewno źle, bo wynik powinien wyjść x∊(0;2)
9 gru 15:06
krystek: Przecztaj uważnie co napisałam o godz 14:47
9 gru 15:09
matema: no i ...

9 gru 15:10
asdf: Nie ma co sprawdzać jak zapisałeś (...)<−1;−∞)
9 gru 15:10
krystek: Odp x∊(0,2)
9 gru 15:11
matema: nie rozumiem
9 gru 15:12
matema: czyli delta nie należy do dziedziny, czy co

9 gru 15:12
9 gru 15:12
matema: czy dziedzina to tylko ta wspólna część x∊(0;2)
9 gru 15:13
9 gru 15:13
krystek: Tak
9 gru 15:14
matema: krystek x<1
9 gru 15:14
matema: mnożę mianownik razy licznik

9 gru 15:15
9 gru 15:15
matema: a co

9 gru 15:15
krystek: Iloraz zastępujesz równoważnym iloczynem.
9 gru 15:16
matema: proszę, rozwiąż to zadanie po kolei, wtedy zrozumię, bo się pogubiłem

9 gru 15:16
9 gru 15:16
matema: no i ten sam wynik
x<2 x>0
9 gru 15:17
krystek: a co napisałeś o 15:14?
9 gru 15:19
krystek: I teraz masz wspólną część i masz odpowiedź , którą podałeś i koniec zad.
9 gru 15:20
matema: no bo mnie zmyliłeś
9 gru 15:20
matema: czyli nie to wszystko jak napisałem, tylko ta wspólna część to dziedzina

9 gru 15:21
matema: mam jeszcze takie zadanie:
| | √x2−4 | | 5 | | 1 | |
d) f(x)= |
| + |
| + |
| |
| | x2+1 | | x2−1 | | √2x−1 | |
też obliczyć dziedzinę
9 gru 15:26
krystek:

Tak.
Przeczytaj uważnie co Ty napisałeś o 15:04. Nie oskarżaj .
9 gru 15:28
krystek: x2−4≥0 i x2−1≠0 i 2x−1>0
9 gru 15:29
matema: nie oskarżam, czyli dziedzina to wspólna część tak ?
9 gru 15:29
krystek: tak
9 gru 15:30
matema: a z pierwszym mianownikiem coś zrobić

9 gru 15:30
krystek: a pomyśl ! Jaka przyjmuje wartość dla każdego x!
9 gru 15:35
matema: a jak mama x
2−4≥0 to liczę delte czy normalnie

9 gru 15:36
krystek: a co to znaczy" normalnie"?
9 gru 15:38
matema: to jest normalnie:
x2≥4
x≥2 x≥−2
9 gru 15:38
krystek: To jest anormalnie
9 gru 15:40
matema: to które dobrze, to z deltą, czy to anormalnie ?
9 gru 15:43
krystek: A jaką dasz odpowiedź do tego co napisałeś.
9 gru 15:43
9 gru 15:44
matema: aha, zapomniałem o wzorach skróconego mnożenia
9 gru 15:52
matema: już rozumiem, ale jak deltę policzę to też dobrze

9 gru 15:52
krystek: ale opanuj nierówności , o 15:04 popełniłeś też karygodny błąd.
9 gru 15:53
krystek: Jak wolisz Δ to licz!
9 gru 15:54
matema: chodzi o wykres

9 gru 15:54
krystek: o zapis
2−x>0 x<0
9 gru 16:01
mata: Jak liczę deltę i to wyrażenie to mi jednak coś innego wychodzi. Możliwe

9 gru 22:00


 Głupi przykład
Głupi przykład
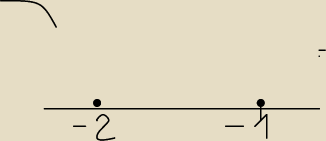 moje rozwiązanie
x2+3x−2≥0
Δ=1
x1=−2 x2=−1
x∊(−∞;−2>u<−1;−∞)
moje rozwiązanie
x2+3x−2≥0
Δ=1
x1=−2 x2=−1
x∊(−∞;−2>u<−1;−∞)
 2−x>0 x<0
2−x>0 x<0














 Tak.
Przeczytaj uważnie co Ty napisałeś o 15:04. Nie oskarżaj .
Tak.
Przeczytaj uważnie co Ty napisałeś o 15:04. Nie oskarżaj .









 x2−4≥0⇔ (x+2)(x−2)≥0 ⇔ gdy dokończ
x2−4≥0⇔ (x+2)(x−2)≥0 ⇔ gdy dokończ


