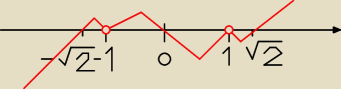
nierówność? m4k: coś mi się rozwiązanie nie pokrywa z odpowiedziami w zadaniu − to jest okej? monotoniczność funkcji:

	2x(x2−2)
f'(x)=		>0 ⇔ 2x(x2−2)(x2−1)2>0
	(x2−1)2

f rośnie w (−√2,−1)U(−1,0)U(√2,+∞) − czy to jest okej?

Ajtek: Jeżeli to jest pochodna to: f'(x)>0 ⇔ 2x(x²−2)>0, ponieważ mianownik (x²−1)² zawsze większy od 0.

m4k: a jeśli x=1 v x=−1 ? czy to nie jest tak, że mianownik nie może być = 0 ? czy źle rozumuje?

ICSP: a dziedzinie kolego ustaliłeś ?

m4k: tak....... przepraszam, ale wstyd... Zapytam jeszcze o coś na przyszłość:

	1
zakładając, że funkcja pierwotna f(x)=ln(x2−1)+		, Df=(−∞,−1)U(1,+∞)
	(x2−1)

	2x(x2−2)
oraz f'(x)=		, Df'=R\{−1,1}
	(x2−1)2

to przy ustalaniu ostatecznych wniosków jaką dziedzinę brać pod uwagę? dziedzinę pierwotną, dziedzinę pochodnej funkcji czy ich część wspólną ?

m4k: odświeżam