 Witam wszystkich
Witam wszystkich  Mam takie zadanie http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D101349846701445%26metadata&access_token=100000605669188%3AAVJ5EH0AKk4Eh_dyjrt1pniA07cTibSdiIRBglzr-Who7g&title=Zadania+nr+2+-+rozszerzony.docx Zadanie nr, 8
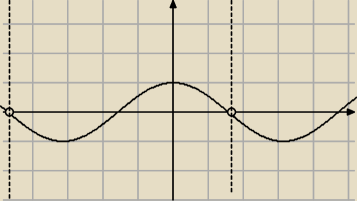
Zacząłem od rysunku i moim zdaniem te rozwiązania mogą być tylko tak położone − jedno ujemne
napewno dla x=−π a dwa kolejne gdzieś z przedziału od −π/2 do π/2
nie wiem czy dobrze myślę, proszę o pomoc i wskazówki
Mam takie zadanie http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D101349846701445%26metadata&access_token=100000605669188%3AAVJ5EH0AKk4Eh_dyjrt1pniA07cTibSdiIRBglzr-Who7g&title=Zadania+nr+2+-+rozszerzony.docx Zadanie nr, 8
Zacząłem od rysunku i moim zdaniem te rozwiązania mogą być tylko tak położone − jedno ujemne
napewno dla x=−π a dwa kolejne gdzieś z przedziału od −π/2 do π/2
nie wiem czy dobrze myślę, proszę o pomoc i wskazówki
 pomoże ktoś ? zad 9 też nie umiem
zacząłem od tego że policzyłem wzór prostej l: y=−x+2 z tego D=(x,−x+2) no i próbowałem z
odległości punktu D od prostej AC tylko że wyszły mi 2 niewiadome
√10a2+10=ax+x+2a−4 gdzie a to współczynnik kierunkowy od prostej AC a x to od punktu D
pomoże ktoś ? zad 9 też nie umiem
zacząłem od tego że policzyłem wzór prostej l: y=−x+2 z tego D=(x,−x+2) no i próbowałem z
odległości punktu D od prostej AC tylko że wyszły mi 2 niewiadome
√10a2+10=ax+x+2a−4 gdzie a to współczynnik kierunkowy od prostej AC a x to od punktu D

 Potrzebuje pomoc przy zadaniach 8,10 i sprawdzenie 11 http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D101349846701445%26metadata&access_token=100000605669188%3AAVJ5EH0AKk4Eh_dyjrt1pniA07cTibSdiIRBglzr-Who7g&title=Zadania+nr+2+-+rozszerzony.docx
Potrzebuje pomoc przy zadaniach 8,10 i sprawdzenie 11 http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D101349846701445%26metadata&access_token=100000605669188%3AAVJ5EH0AKk4Eh_dyjrt1pniA07cTibSdiIRBglzr-Who7g&title=Zadania+nr+2+-+rozszerzony.docx






 11/
Pp=a2*sin30o ⇒ a=...... h= 2r
Pp= a*h ⇒ h= ... ⇒ r=....
hb= .... z tw. Pitagorasa
11/
Pp=a2*sin30o ⇒ a=...... h= 2r
Pp= a*h ⇒ h= ... ⇒ r=....
hb= .... z tw. Pitagorasa
| 1 | ||
Pb= 4* | a*hb=.... | |
| 2 |

 zadanie 8
zadanie 8
| −3π | π | |||
3cos2x−(p+1)cosx=0 i x∊( | ; | ) | ||
| 2 | 2 |
| p+1 | ||
cosx= | ||
| 3 |
| π | ||
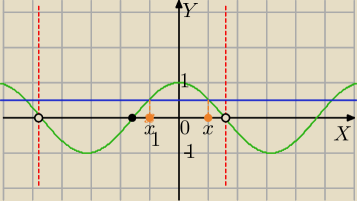
cosx=0 dla x=− | i jest ujemne , niezależnie od wartości p | |
| 2 |
| p+1 | ||
Rysujemy prostą poziomą y= | , aby przecinała odpowiednio wykres w 2 punktach. | |
| 3 |
| p+1 | p+1 | |||
dla | >0 i | <1 otrzymamy podobną sytuację | ||
| 3 | 3 |



| |a−3b−4| | |
=√10 | |
| √1+9 |

 opuszczenie wartości bezwzględnej 10=I3y−x+4| http://www.zadania.info/d541/4158930
u mnie wyszło 10=|x−3y−4| wiem że to to samo ale jak opuścić wartość bezwgledną
opuszczenie wartości bezwzględnej 10=I3y−x+4| http://www.zadania.info/d541/4158930
u mnie wyszło 10=|x−3y−4| wiem że to to samo ale jak opuścić wartość bezwgledną  Niech ktoś mi to wytłumaczy, nie koniecznie Eta
Niech ktoś mi to wytłumaczy, nie koniecznie Eta 
