matura PuRXUTM: Witam mam takie zadanko Proszę o sprawdzenie rozwiązania

	2+x
Dana jest funkcja f(x)=		gdzie x∊R\{4}:
	4−x

a) Wyznacz wszystkie punkty należące do wykresu funkcji f, których obie współrzędne są liczbami pierwszymi. (Liczby pierwsze chyba nie mogą być ujemne, więc wyszło mi tak A=(2,2) B=(3,5) b) Podaj zbiór tych argumentów, dla których funkcja f przyjmuje wartości nieujemne pierwsze narysowałem wykres ale zorientowałem się że wystarczy rozwiązać nierówność f(x)≥0 i wyszło mi że dla x∊<−2;4)

	|f(x)|
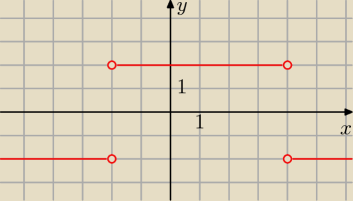
c) Naszkicuj wykres funkcji g, jeśli g(x)=		narysowałem tak ( rysunek wyżej )
	f(x)

ZKS:

Aga1.: b) dobrze c) g(x)=1 lub g(x)=−1, a nie g(x)=2 lub g(x)=−2

ZKS: Znaczy wykres jest źle bo zbiór wartości g(x) jest równy y ∊{−1 ; 1} a nie tak jak u Ciebie −2 ; 2.

PuRXUTM: dzięki Aga, kurde dobrze myślałem a źle narysowałem...

PuRXUTM: Tobie też dziękuje niewidoczny ZKS

ZKS:

PuRXUTM: http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D101349846701445%26metadata&access_token=100000605669188%3AAVJ5EH0AKk4Eh_dyjrt1pniA07cTibSdiIRBglzr-Who7g&title=Zadania+nr+2+-+rozszerzony.docx w sumie nie ma co przepisywać zadań, będe pisał moje odpowiedzi w drugim wyszło mi k>6

ZKS: .

PuRXUTM: 3a) α=60⁰

ZKS: Tego nie sprawdzę Ci bo bym musiał nad tym posiedzieć z 10 minut pewnie co najmniej.

PuRXUTM: nie ma sprawy, nie musisz jak nie masz ochoty dziękuje za wcześniejsze Mam takie pytanie do 3b) czy było coś takiego że

	1
(dł. odcinka łączącego środki ramion trapezu) : (obwód trapezu)=
	4

bo coś tak mi się kojarzy...

aniabb: jeśli trapez był opisany na okręgu

PuRXUTM: czyli tutaj nie... dzięki Ania

Aga1.: a) Ok. b)9.

ZKS: Nie o to chodzi czy mam ochotę czy nie tylko o to że nie lubię akurat tych działów topornie mi idą średnio je zawsze lubiłem.

Aga1.:

	a+b
Środkowa =		, a, b −podstawy trapezu.
	2

PuRXUTM: dzięki Aga, b) też mi wyszło 9

aniabb: 3b możesz też z podobieństwa trójkątów... będzie 9cm

PuRXUTM:

	(7+x)*2√3		(x+11)*2√3
ja to zrobiłem z pól że Pc=P1 + P2=		+		gdzie x to ten
	2		2

szukany odcinek

aniabb: wszystkie drogi prowadzą do Rzymu

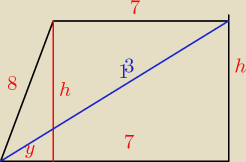
Aga1.: A ja liczyłam y z układu h²=8²−y² h²=13²−(y+7)²

PuRXUTM: hahahah tylko niektóre przez np. Moskwę

PuRXUTM: wpadnę jeszcze wieczorem do zobaczenia