Wyznacz dziedzinę wyrażenia heretic: Uczę się do sprawdzianu. Najlepiej jakby ktoś mógł napisać rozwiązanie i ogólnie jak do tego doszedł a ja przeanalizuje. Wyznacz dziedzinę wyrażenia: log_3x+1(x²−4)− log_3x−2(6x−2)

xyz: z definicji logarytmu podstawa logarytmu musi być większa od 0 i różna od 1, natomiast liczba logarytmowana musi być większa od 0. Wystarczy policzyć odpowiednie nierówności

Eta: ......

xyz: 3x+1>0 3x+1≠1 3x−2>0 3x−2≠1 x²−4>0 6x−2>0 musisz znaleźć x−ksy które spełnają wszystkie te nierówności i to będzie dziedzina.

pawo: Jak znaleźć te x? Tylko sie nie denerwuj, szybko sie ucze

heretic:

	1
Obliczyć? Czyli co do pierwszego 3x>−1 => x>−		?
	3

heretic: Czy dobrze kombinuję?

heretic: Jest jakaś szansa, że ktoś to rozwiąże?

xyz: tak dobrze myślisz, właśnie tak trzeba to zrobić i jak wyznaczysz wszystkie x to musisz wziąć część wspólną wszystkich wyników i to będzie dziedzina

heretic: Więc:

	1
x>
	3

x≠0

	2
x>
	3

x≠1 x>2

	1
x>
	3

	1
Więc x∊ {		; 2}
	3

Zgadza się?

heretic: Can You help me? Tylko pytam A od wczoraj już się mecze z tym zadaniem

Jakub: Po pierwsze źle rozwiązałeś nierówność x²−4>0. Zrób jak tutaj 102 Po drugie bierz część wspólną rozwiązań. Część wspólna tych wypisanych przez ciebie rozwiązań to przedział (2,∞). Najlepiej zaznacz to wszystko na osi liczbowej, aby zobaczyć jaka jest część wspólna. Najpierw jednak x²−4>0.

heretic: Ok, z tym już sobie poradzę, dzięki Pozdrawiam

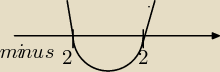
xyz: x²−4>0 x²−2²>0 (x−2)(x+2)>0 miejsca zerowe: x=2 x=−2 współczynnik przy x² jest dodatni, więc parabola "uśmiechnięta" szukamy rozwiązań większych od 0, więc x∊(−2,2)

heretic: Dziedzina to część wspólna tak?

xyz: tak część wspólna rozwiązań wszystkich tych twoich 6 równań

heretic: x=2 x=−2 czy x>2 x>−2 ?

xyz: a raczej nierówności

xyz: chodzi ci o rozwiązanie nierówności x²−4>0?

heretic: tak

xyz: x=2 i x=−2 to są miejsca zerowe, bo rozwiązujesz tą nierówność dokładnie tak samo jak równość, tylko nie kończysz na wyznaczeniu x₁ i x₂, ale musisz jeszcze narysować wykres i zaznaczyć w jakim przedziale jest on nad osią(bo ...>0)

xyz: no więc ostateczne rozwiązanie tej nierówności jest tak jak piszesz x<−2 i x>2.

heretic: troche zakręciłeś, ale robie tak jak mówisz, dzięki za wkład no i za tłumaczenie oczywiście

xyz: