Stereometria kodobi: 13. Na stole stoi szklanka pełna wody mająca kształt walca obrotowego o promieniu podstawy r, oraz wysokości h (h ≥ 2r). Nachylamy szklankę o kąt φ względem stołu, przy czym 0 ≤ φ ≤ 0,25π. W następstwie czego część wody wylewa się ze szklanki. Ile wody pozostało w szklance?

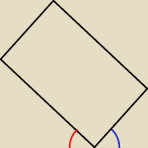
MQ: Zadanie niejasne: "Nachylamy szklankę o kąt φ względem stołu". Gdzie jest to φ? Czerwone czy niebieskie?

kodobi: Sam się nad tym zastanawiałem. Wg mnie to w takiej sytuacji czerwony kat. Bo niebieski jest tak jakby pod szklanką. Na tej stronie o ile dobrze rozumiem koleś twierdzi, że to powinien być kat między wysokością walca stojącego normalnie, a "bokiem" pochylonego walca. http://www.matematyka.pl/100394.htm

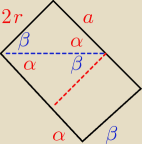
MQ: 2r/a=tgα lub 2r/a=ctgβ Wyleje się połowa objętości walca o promieniu podstawy takiej samej jak szklanka i wysokości a. Czyli pozostanie (h−a)*pole podstawy

	h−a
Czyli szukasz proporcji
	h

W zależności, który kąt (α czy β) bierzesz pod uwagę −− wg mnie β −− tak liczysz z tg lub ctg wysokość a.

MQ: Poprawka Zostanie (h−a/2)*pole podstawy, więc szukamy proporcji:

h−a/2
h

Eta: @MQ Coś ostatnio trafiają Ci się te "szklanki" ( ciekawe z jakim napojem? Pozdrawiam

kodobi: @MQ Skąd wiemy, że wyleje się połowa objętości?

MQ: Śliwowiczka ew. łiskaczek

MQ: Bo to co jest u góry (nad niebieską płaszczyzną", po obróceniu o 180^o pokryje się z tym co jest u dołu.

kodobi: Aaa sory już wiem (Czytanie ze zrozumieniem się kłania)

kodobi: Dzięki wielkie wszystko już rozumiem Szkoda, że nie można stawiać piwa albo czegoś podobnego

MQ: Można! O tak:

aniabb: albo tak https://matematykaszkolna.pl/strona/serwer.html