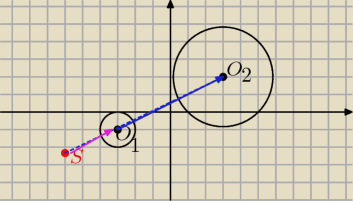
jednokładność PuRXUTM: W jednokładności o środku S i skali k obrazem okręgu o równaniu (x+3)²+(y+1)²=1 jest okrąg o równaniu (x−3)²+(y−2)²=9. Oblicz współrzędne środka S jednokładności Jeśli można to proszę o pełne rozwiązanie bo nie ogarniam tego, kiedyś to robiliśmy podobno w czerwcu, nie umiem tego...

MQ: Skalę jednokładności dostajesz od razu z promieni okręgów: r₂=k*r₁ r₁=1 r₂=3 Jak znasz skalę, to ze środków okręgów łatwo już dostać S: SO₂^→=k*SO₁^→ O₂ −− środek oręgu − obrazu O₁ −− środek okręgu − źródła

Basia: okrąg 1: A(−3; −1) r₁ = 1 okrąg 2: B(3; 2) r₂ = 3

	r2
zatem |k| =		= 3 ⇒ k=3 lub k= −3
	r1

S(x,y) dla k=3 SB^→ = 3*SA^→ SB^→ = [3−x; 2−y] SA^→ = [−3−x; −1−y] czyli [3−x; 2−y] = 3*[−3−x; −1−y] 3−x = −9 − 3x 2x = −12 x = −6 2−y = −3−3y 2y = −5

	5
y = −
	2

czyli może to być jednokładność o środku S(−12; −⁵₂) i skali k=3 przypadek k= −3 rozważ analogicznie

Aga1.: r₁=1,r₂=3 k=3 lub k=−3 S=(x,y) O₁=(−3,−1) O₂=(3,2) SO₂→=3*SO₁→ [3−x,2−y]=3[−3−x,−1−y] 3−x=−9−3x i 2−y=−3−3y S= Rozpatrz drugi przypadek, gdy k=−3.

PuRXUTM:

	3		1
dla k=−3 wyszło mi x=−		y=−
	2		4

Basia: dobrze

PuRXUTM: dzięki wszystkim, coś tam zakapowałem