trapez równoramienny wpisany w okrąg Zuzia: W trapezie równoramiennym wpisano okrąg. Oblicz obwód i pole trapezu jeśli jego: a) ramię ma długość 6cm, a promień okręgu jest równy 2,5cm. b) podstawy mają długość 4cm i 16cm, c) kąt ostry ma miarę 60 stopni, a promień okręgu opisanego na tym trapezie jest równy 1cm.

Zuzia: Pomoże ktoś

camus: a) Mamy okrąg wpisany w trapez, więc z właśności czworobokół opisanych na okręgach, mamy c+c = a+b , gdzie c to długość ramienia, a i b kolejno podstawa dolna i górna a+b=6+6=12 Stąd Obw = a+b+c+c=12+12=24

	(a+b)*h
P =		//nasze h tutaj to inaczej 2r, r−długość promienia
	2

	12*5
P=		=30
	2

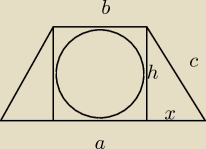
camus: b) z tej samej własności c+c=a+b 2c = 4+16=20 c=10 Obw = 20+20=40

	a−b
x =		= 6
	2

z tw Pitagorasa 10² = 6² + h² h²= 100−36=64 h=8

	20*8
P =		=80
	2

camus: c) z tym to już sobie poradzisz, pownioskuj trochę i pomyśl

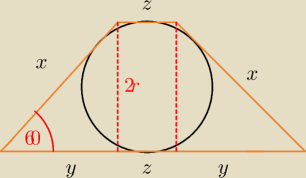
wredulus_pospolitus: odkopuję odkopywany przez kogoś tam c) krok 1: najistotniejszy jest rysunek: krok 2: z funkcji trygonometrycznych obliczasz 'x' krok 3: z funkcji trygonometrycznych obliczasz 'y' krok 4: z tw. o sumie przeciwległych boków czworokąta opisanego na okręgu obliczasz 'z' krok 5: podstawiasz do wzorów, aby wyliczyć pole i obwód

icoverty: możecie podpowiedzieć jak zrobić to c? bo podpunkty, a i b sobie rozwiązałem, ale właśnie c już nie bardzo nawet wiem jak ugryźć

icoverty: o dzieki wredulus

icoverty: dobra, troszkę się zapędziłem, bo R dotyczy tutaj okręgu opisanego a nie wpisanego w trójkąt