kilka zadań z ciągów Michał kowolik: 1. Suma n wyrazów ciągu arytmetycznego wynosi S_n=n² − 5n. więc A ) a_n= −84+4 B ) r= −6 c a₁=2

	n2−n−12
2. Dany jest ciąg, w którym b4=		wobec tego b4<0 dla
	n+7

a: n∊{−3,−2,0,1,2,3,4} B: n∊<−3,4>, C: n∊{0,1,2,3} Dziękuję

think: ad 1 S₁ = 1² − 5*1 = 1 − 5 = −4 = a₁ S_n − S_{n − 1} = a_n a_n = n² − 5n − [(n − 1)² − 5(n − 1)] = n² − 5n − [n² − 2n + 1 − 5n + 5] = 2n −6 r = S₂ − 2S₁ = 2² − 5*2 − 2*(−4) = 4 − 10 + 8 = 2

Aga1.: 1. a₁=S₁=−4, S₂=a₁+a₂=−6 , stąd a₂=−2 r=a₂−a₁=−2+4=2 a_n=−4+(n−1)*2=−6+2n

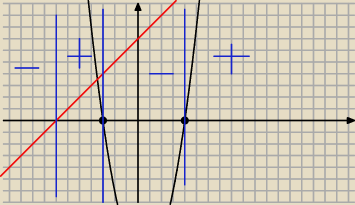
think: ad 2 n² − n − 12 Δ = 1 + 48 = 49 ⇒ √Δ = 7 n₁ = 4 n₁ = −3 iloraz ma być ujemny a to mamy dla n∊(−∞ −7)∪<−3, 4> ale ponieważ n jest indeksem ciągu, to oznacza że interesują nas tylko n∊ℕ₊ zatem odpowiedzią będą {1, 2, 3, 4} ponieważ ani w pierwszym ani w drugim nie znalazłam poprawnej odpowiedzi to jestem zaintrygowana....

Aga1.: 2)

n2−n−12
	<0/*(n+7)
n+7

n²−n−12<0 n∊(−3,4) i n∊N⁺ Odp. n∊{1,2,3}

think: ano fakt nie zauważyłam że tam nierówność jest ostra