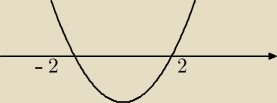
Oblicz monotonicznośc i ekstrema titi: Proszę bardzo o pomoc!

	x		1
f(x)=		+
	4		x

1) D∊R−{0}

	1		1
2)f'(x)=		−
	4		x2

3)f'(x)=0

1		1
	−		=0
4		x2

1		1
	=
x2		4

x²=4 (x−2)(x+2)=0 x=2 v x=−2 5) f(x) rosn. dla x∊(−∞,−2)u(2,∞) f(x) mal. dla x∊(−2,2) 6)max. dla −2 min. dla 2 W odpowiedzi jest inaczej. Zapewne pomyliłem się od p. 3) tak? Prosiłbym bardzo o wyjaśnienie co zrobiłem źle

krystek: Nie wyrzuciłeś zera

titi: W odpowiedzi jest Rosnąca w (−2,0), (0,2);malejąca w (−∞, −2), (2, +∞), minimum w −2, maximum w 2

titi: To może w odpowiedzi jest źle? Jeżeli wyrzucę zero to f mal. dla x∊(−2,0)u(0,2)

krystek: Nie widzę błędu , może nie zauważam Ale wyjściowa f dobre zapisana?

titi:

	x		1
Na 100% dobrze f(x)=		+		. Mam kolokwium w piątek i ciągle rozwiązanie nie daje mi to
	4		x

spokoju...

krystek: wszystko ok

titi: Oki mam nadzieję, że to prowadzący się pomylił. W sumie napiszę do niego maila

krystek: Czasem w"rozpędzie" następują pomyłki , nie wynikają one z braku wiedzy.