stożek. proszę o pomoc jadzia: W stozek ktorego przekrojem osiowym jest trojkat rownoboczny o boku 4 wpisano szescian( szescian jest wpisany w stozek, jezeli cztery jego wierzcholki naleza do podstawy a pozostale cztery do powierzchni bocznej stozka).Oblicz dlugosc krawedzi tego szescianu

irena_1: a− krawędź sześcianu Narysuj trójkąt równoboczny ABC a w nim prostokąt KLMN, którego jeden, bok KL,leży na podstawie AB, a 2 pozostałe wierzchołki na ramionach − M na BC, N na AC. Bok KL prostokąta zawarty w podstawie trójkąta to przekątna podstawy sześcianu, bok LM to krawędź sześcianu. Masz trójkąt prostokątny LBM, w którym |LM|=a

	4−a√2
|LB|=
	2

	a
ale |LB|=
	√3

a		4−a√2
	=
√3		2

4√3−a√6=2a 2a+a√6=4√3 a(√6+2)=4√3 a(√6+2)(√6−2)=4√3(√6−2) a(6−4)=4√18−8√3 2a=12√2−8√3 a=6√2−4√3

Bogdan:

	1
h =		a√3
	2

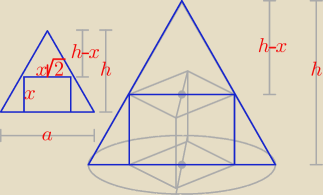
Korzystamy z trójkątów podobnych:

a		h		a		1   a√3 2
	=		⇒		=
x√2		h − x		x√2		1   a√3 − x 2

1		1		2
	a2√3 − ax =		ax√6 / *		⇒ a√3 − 2x = √6 ⇒ a√3 = x(√6 + 2)
2		2		a

	a√3
x =		.
	√6 + 2

	4√3		√6 − 2
Dla a = 4: x =		*		= ....
	√6 + 2		√6 − 2