funkcja adaś: Szkicując odpowiedni wykres funkcji rozwiąz nierownosc: x²−|x−4|≥−2 nie mogę tego sobie wyobrazić jak to będzie wyglądało na wykresie, co ma pokryć modułem wartości bezwzględnej na rysunku ?

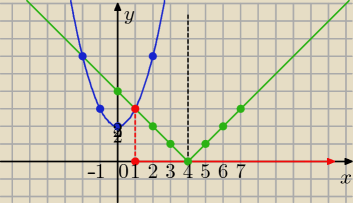
Eta: −|x−4|≥ −x²−2 /*(−1) |x−4|≤ x²+2 zielony wykres y= |x−4 | , niebieski wykres y= x²+2 Odp te x, dla których wykres zielony jest pod wykresem niebieskim x∊ <1,∞)

adaś: Dzięki bardzo Eto, lecz chyba jeszcze tu czegoś nie rozumiem co do rozwiązania nierówności ,to będzie x²−x−4+2≥0 x²−x−2≥0 oraz x²+x+4+2≥0 x²+x+6≥0

Eta: Podałam Ci rozwiązanie graficzne ! algebraicznie: 1/dla x≥4 x²−(x−4)≥−2 ⇒ x²−x+6≥0⇒(x+2)(x−3)≥0 x∊ (−∞, −2> U <3,∞) i x≥4 wybierasz część wspólną x∊ <4,∞) 2/ dla x<4 x²−(−x+4)≥ −2⇒ x²+x−2≥0 ⇒(x+2)(x−1)≥0 x∊(−∞,−2> U <1,∞) i x<4 i część wspólna x∊<1,4) odpowiedzią jest x należący do sumy obydwu przedziałów x∊<4,∞) U <1,4) ⇒ x∊<1,∞) −−− co też widać na wykresie Echh adaś kiedy ty to wreszcie pojmiesz ?

adaś: nie wiem jeszcze jak dochodzisz do tego zielonego wykresu ,tzn. jak dojść do punktów zielonych. prawdopodobnie z tego : x²−x+6≥0 x²+x−2≥0 obliczasz wierzchołek tak ?

krystek: \ Niebieska to y=x²+2 Zielona o y=Ix−4I

adaś: nic nie rozumiesz ,tłumaczysz nie umiesz

ZKS: |x − 4| ≤ x² + 2 x − 4 ≤ x² + 2 ∧ x − 4 ≥ −x² − 2 x² − x + 6 ≤ 0 ∧ x² + x − 2 ≥ 0 Rozwiązać nierówności bierzesz część wspólną i masz odpowiedź.

ZKS: Przepraszam nie zauważyłem że narysować wykres trzeba. Wiesz jak wygląda wykres y = |x − 4|?

adaś: chodzi mi o to jak dojść do wykresu zielonego ,jak dojść do punktu (1;3) , (2;2) ,(3;1), (4;0)

adaś: jak mam to obliczyć na kartce i nanieść

krystek: y=Ix−4I i wstawiaj podane przez Ciebie wartości!11 x=1⇒y=I1−4I=I−3I=3

adaś: i tak nie wiem co po kolei mam w takich przykładach zrobić Eta napisała ale niezrozumiale dla mnie mógłby ktoś W SKRÓCIE napisać jeszcze raz schemat działań

krystek: Oj Adas Adaś , ja tłumaczyć nie umiem, Eta pisze niezrozumiale dla Ciebie, zastanów się Dziecko, co piszesz.

Eta:

adaś: dobrze by było jak by ktoś mi napisał w punktach co się robi w takim przykładzie, bo wszystko się mi miesza i zapominam

Eta: @adasia Na ile % zaliczyłeś próbną maturę ? tylko napisz prawdę! To będziemy wiedzieć jak Ci pomóc .... abyś dobrze ją zdał !

krystek: 19:24 Eta Tobie wszystko wyjaśniła. Krzysiek "powieści" Tobie pisał . Poczytaj ze zrozumieniem .

adaś: to jest nie ważne, na pewno ją zaliczełem i dzięki Wam poczęści wiec Wasz wysiłek nie poszedł na marne , możecie mi pomóc teraz jak napiszecie mi to co jest →4 gru 2012 21:27

krystek: Problem Adasia , to ten,że zaczął na tym forum od trudnych zadań i przeskakiwał z zadaniami z działu na inny dział. Tak sądzę.

adaś: proszę tylko o napisanie jeszcze raz w punktach od czego mam zacząć , bo się już zaplątałem na maksa teraz

Eta: Nie odpowiedziałeś na moje pytanie

krystek: 21:19 masz podane jak liczyć.

Eta: https://matematykaszkolna.pl/strona/1376.html Tu masz wyjaśnione

Eta: Moja propozycja: najpierw poczytaj co podaje Jakub do każdego działu Dopiero wtedy zabieraj się za rozwiązywanie podobnych zadań

Eta: Już Ci 100 razy pisałam: "najpierw naucz się pływać" zanim wejdziesz na głębszą wodę! Ale Ty nie słuchasz tego co Ci radzimy i stąd masz problemy

adaś: Krystek mi chodzi o całe zadanie czyli →4 gru 19:07 , prosił bym o napisanie w punktach co się robi po kolei , koło 40% , ale przerabiając tylko działy z funkcji , resztę to nie pamiętałem i pisałem jak uważałem i nawet niektóre dobrze, nie byłem w stanie sobie całego materaiału podstawowego powtórtrzyć tak szybko. Eta zrób tak jak mówie i zobaczę czy wtedy będę już wiedział o co chodzi.

Eta: https://matematykaszkolna.pl/strona/1376.html Tu masz ten wykres!

krystek: Nic już nie napiszę . Wszystko masz . Eta podała Tobie odsyłacz do strony ,która zawiera potrzebne treści .

adaś: no dobrze ja ten wykres bardzo dobrze rozumiem ale nie o to mi chodzi, nie rozumiesz już piszę co bym chciał najbardziej jeżeli jesteś w stanie

adaś: ok w takim razie nie

Eta: https://matematykaszkolna.pl/strona/1379.html Niebieska parabola podobnie tylko przesunięta w górę W(0,2)

Eta: Taaakiego "przypadku" to nie miałam !

krystek: Ja tez . Adaś możesz podać do jakiego typu szkoły średniej uczęszczasz?

adaś: nie

Eta:

Eta: Jak widać........ to nawet Syzyf miał lżejszą pracę

adaś: aha

Piotr: widzę, że nic sie nie zmieniło.

adaś: ::

ZKS: Zadam jedno pytanie chodzisz do szkoły czy nie? Pytam się poważnie bo chcemy wiedzieć czy jesteś samoukiem lub może coś innego?

adaś: samouk już pisałem

ZKS: A skąd ja mam to wiedzieć nie śledzę Twoich postów każdorazowo więc stąd moje pytanie. Wiesz jak rysować podstawowe wykres typu y = |x| oraz przesuwać wykresy o wektor?

adaś: wiem jak rysować , chyba po prostu od początku nie poprawnie zrozumiałem wartość bezwg. w zadania gdzie trzeba rysować wykres i z tego powodu takie problemy się ciągną. koniec tematu .

Eta: No i "koniec"

Ajtek: No to chyba sobie pomogłeś 172407. Obserwuję Ciebie od sierpnia/września, wcześniej nik szklanka. Jesteś samoukiem. Cieszy mnie to i Twój zapał. Niestety, nie uczysz się, a to mnie smuci. Pisząc "omijam szerokim" łukiem, miałem na myśli, że nie jestem Tobie w stanie pomóc. Ten wątek tylko to potwierdził. Jeżeli Twierdzisz, że Eta i krystek nie potrafią tłumaczyć, to ja również nie umiem. A Twoje zachowanie z linku.... no cóż niech inni to ocenią.

adaś: mam nadzieje ze to miales na mysli. dobrze wiemy jakie jest nauczanie w szkołach to nie moja wina ze nie nierozumiem jednaki chce zrozumiec dla mnie jest nie zrozumiałem to co pisza dla innych moze tak.

asdf: @adaś Doceń to, że ktoś Ci tu pomaga, bo niektórzy nawet odpłatnie by zrezygnowali, a ty masz takie rzeczy za darmo. Zacznij wyciągać wnioski i słuchaj tego co Ci piszą − PODSTAWY! Dlaczego ty próbujesz rozwiązać taką wartość bezwzględną, jeżeli (według mnie − dobrze, żebym się mylił) miałbyś nawet problemy z taką: |x − 3| < −3 ....

Eta: x∊∅

asdf: I dlaczego ty zganiasz na szkolnictwo? Żyjemy w XXI wieku i jak się czegoś nie rozumie, idzie się po dobrą książkę do księgarni/biblioteki (wczesniej mozesz zapytac ludzi na forum) i się uczysz... @Eta dobrze adaś

Krzysiek : Adas. TO ze nie mozesz pojac roznych rzeczy wcale ale to wcale nie upowaznia Cie to tego aby sie odnosic tak jak do Ajtka czy Krystka . A co by bylo jak bys sie pomylil i to TY bys dostal wpierdol . Mysle ze chyba w tym momencie nie byles soba . Wiesz ile ludzie placa za takie rzeczy takie jakie Ty masz tutaj za darmo?.Pomysl sobie ze nie stac Cie byloby na to . Bierzesz sie za rzeczy trudne i potem flustracja . Wszyscy CI pisali najpierw podstawy przede wszyskim podstawy. Musisz to zrozumiec ze bez tego ne ruszysz zmiejsca Trzeba sie z tym pogodzic ze jesli sie zaniedbalo tyle lat nauki to teraz sie tak szybko nie nadrobi. Jesli tego nie zauwazyles to zobacz jaki poziom wiedzy ma Ajtek czy Eta Mila Ania Krystek Piotr i inni ktorzy TObie chcieli naprawde pomoc a takimi odzywkami jak do Ajtka tylko ich zrazasz do siebie . Popatrz wszyscy potracili do Ciebie cierpliwosc a mimo to pomagaja . No jakie jest nauczanie w szkole jesli masz przuyklad tych ludzi co pisalem o nich . Wiec moz e zastanowilbys sie nad tym zeby ta mature przelozyc na nastepny rok i zdal jak dobrze bo kiedys pisales ze chcesz isc na studia . Nie wiem jak teraz czy mozna zdac innne przedmioty a np matematyke za rok czy trzeba zdawac wszystko Eta napisala CI zebys najpierw zagladal na lewa strone co tam jest napisane . Gdybys zagladal tam wczesniej pewnie problemow bylo by o wiele mniej i to duzo mniej . Teraz do rzeczy. Postaraj sie to zapamietac. Jesli masz narysowac wykres funkcji beda przyklady dla zobrazowania y=|x²−5x−6| zobacz ze jest cala w w artosci bezwzglednej to rysujesz ta funkcje ktora jest w w artosci bezwzgladnej czyli x²−5x−6 (nawet mi sie udal przyklad ) i to co jest pod osia OX odbijasz nad os Ox . Jak juz odbijesz to nad os OX to wez gumke i wymaz to co zostalo pod osia. Mmasz juz wykres tej funkcji y=|x²−5x−6| . Proste ? proste . Tak jak pisal Pw wartosc bezwzgledna gnebi liczby ujemne . Wiec kazda taka funkcje postaci y=|cos tam | to rysujesz wykres tej funkcji co jest w module i ta czesc co jest pod osia OX przenosisz nad os OX. maz narysowac wykres funkcji y=|x−4| to rysujesz wykres y=x−4 i to pod osia ox dajesz nad os . i masz wykres tej funkcji y=|x−4| . Teraz popatrz na rysunek ETY (ten zielony ) . jest taki sam jak ten y=|x−4| −tylko sam sobie narysuj wedlug tego co napisalem . Po drugie . Adas nie rowiazales do konca tego co dalem CI zebys rozwiazal w poprzednim linku . Za podziekowana dziekuje ale jakbys to zrobil to teraz nie mialbys problemow z rozwiazaniem tego zadania . Wrocmy jeszcze na chwile do tej funkcji y=|x²−5x−6| to jesli jeszce do tej pory nie rozumiesz jak to narysowac to zgodnie z definicja wartosci bezwzglednej |x| =x dla x≥0 nas ze x to x²−5x−6 to |x62−5x−6|=x²−5x−6 dla x≥0 wiec narysuj wykres tej funkcjiy= x²−5x−6 Ale tez definicja wartosci bezwzglednej mowi nam ze |x|=−x dla x<0 to jesli nasze x to x²−5x−6 wiec |x²−5x−6| dla x<0 =−(x²−5x−6)=−x²+5x+6 wobec tego na tym samym rysunku narysuj wykres funkcji y=−x²+5x+6. Jak narysujesz to wez gumke i wszystko to co jest pod osia OX wymaz . ZObacz czy czasami nie otrzymales tego samego to co CI pisalem pierwszym sposobem .Mysle ze teraz juz bedziesz wiedzial . na razie koniec

Krzysiek : teraz chciales dojsc do tego zielonego wykresu . To zobacz co chciales zrobic na swoj post z godz 21,02 Wykresem zielonym sa linie proste a TY z linii chchciales zrobic parabole bo przeciez tam napisales funkcje kwadratowe . Wiec zobacz co napisal/a CI Krystek 0 21<05 i TY mowisz ze nie umie tlumaczyc Natomiast jesli masz narysowac cos takiego −tez przyklady y= x²−5|x|−8 tutaj juz nie masz calej funkcji w wartosci bezwzglednej tak jak poprzednio tylko jeden powiedzmy tak sobie skladnik Tutaj tez definicja wartosci bezwzglednej bedzie dzialac . Teraz z definicji |x|=x dla x≥0 to nasza funkcja dla x≥0 ma postac x²−5x−8 czyli wykresem tej funkcji dla x≥0 jest ta czesc paraboli dla x≥0 czyli zera i na prawo od zera czyli do ∞ natomiast |x|=−x dla x<0 to dla x<0 nasza funkcja ma postac y=x²−5*(−x)−8 czyli x²+5x−8 ale tylko jej ta czesc od 0 do −∞ Teraz zobacz na wzor y=x²−5|x|−8 mamy tutaj a=1 bo jest x² b=−5 a takze c=−8 . teaz co nam mowi to −8 Tyle ze wykres tej funkcji przetnie os OY wlasnie w −8 . Czyli te dwie czesci paraboli spotkaja sie w y=−8 na wykresie . Widzisz analogie to funkcji liniowej Tam byla taka postac y=ax+b gdzie b byl to wlasnie punkt przeciecia sie wykresu z osia oY tak samo w funkcji kwadratowej wspolczynnik c jest to punkt przciecia sie paraboli z osia OY. Tutaj mielismy samo |x| ktorej miejscem zerowym jest zero . Teraz najwiekszy Twoj problem jest ten ze jak masz np |x−4| to ta wartosc zeruje sie nie w 0 tylko w 4 bo x−4=0to x=4 teraz popatrz dla samej |x| mozesz zapisac =x dla x≥0 ale juz tutaj nie bo |x−4| ≠ x−4dla x≥0 bo np dla x=1 bedzie |1−4|=|−3| a ona jest ujemna wobec tego opuszczajac wartosc bezwzgledna nalezy zmienic znak i byloby |x−4|=−(x−4)=−x+4 ALe jesli napiszemy ze |x−4|=x−4 dla x≥4tak jak wyliczylismy to zobacz dla x=4 to |x−4|=|4−4|=|0|=0 jest rowne zero −jest teraz dla x=np8 to bedzie |x−4|=|8−4|=|4| dodatnia nie zmieniam znaku =4 >0 Teraz widzisz gdzie robisz blad . Musisz zapisac dla jakich x_ow ≥0 badz x<0 a nie ze napiszesz lub nie tak jak tutaj z godz 19. 40 Juz CI pokazalem z edla x<4 musisz zmienic znak opuszcajac wartosc bezwzgledna To teraz juz nie bede tego rozpisywal tylko popatrz na post ETY z godz 19.58 i zobacz co ona tam napisala 1dla x≥4 itd ....Przeanalizuj to cale dobrze . Poza tym zzobacz ze te funkcje dla przedzialow masz tez w postaci iloczynowej i masz za darno miejsca zerowe , Takze caluj w rece z to. Wiec narysuj te wykresy i zobacz czy rozwiazanie sie zgadza . Nalepiej na forum . NO ale zrobisz jak uwazasz. A co do szkoly to ja sie domyslam jesli on sie uczy sam . jesli tak jest to chwala mu za to Naprawde to narysuj . ja wracam z praco po 23 wiec moze ktos predzej sprawdzi .

Basia: adasiowi się należało, ale nieśmiało zwracam uwagę, że w przedziale (−∞; −2) też zielony jest pod niebieskim