Okręgi... Mateusz. X: 1.Na okręgu o promieniu r opisano trapez którego kąty ostre mają miary α oraz β. Oblicz pole trapezu. 2.Oblicz długość promienia okręgu opisanego na trójkącie o bokach 5x8x10. 3.W okrąg o promieniu 5 wpisano trójkąt którego kąty mają miarę 20, 50, 110. Oblicz pole tego trójkąta. 4. W trójkącie kąty mają miary α, β, γ a bok lezący na przeciw kąta α ma długość a. Oblicz długość promienia okręgu wpisanego w ten trójkąt.

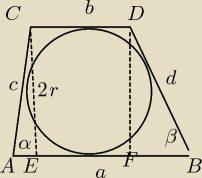
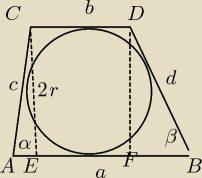AS: Zad.1 Pole trapezu wyraża się wzorem P = 0.5*(a + b)*2*r = (a + b)*r Ale w czworokącie opisanym na okręgu zachodzi a + b = c + d Wobec tego nasze pole ma postać P = (c + d)*r Z ΔACE: 2*r/c = sin(α) ⇒ c = 2*r/sin(α) Z ΔBDF: 2*r/d = sin(β) ⇒ d = 2*r/sin(β) Podstawiam do pola P = (2*r/sin(α) + 2*r/sin(β))*r = 2*r²*(1/sin(α)+ + 1/sin(β)) W zadaniu 2 i 3 wykorzystaj tw.sinusów