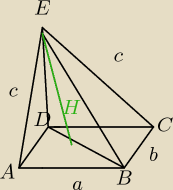
 Podstawą ostrosłupa o równych krawędziach bocznych i wysokości H jest prostokąt o bokach
długości a i b. Oblicz pole przekroju ostrosłupa płaszczyzną przechodzącą przez jedną z
przekątnych podstawy i równoległą do krawędzi bocznej.
Czy chodzi tutaj o trójką BDE?
Podstawą ostrosłupa o równych krawędziach bocznych i wysokości H jest prostokąt o bokach
długości a i b. Oblicz pole przekroju ostrosłupa płaszczyzną przechodzącą przez jedną z
przekątnych podstawy i równoległą do krawędzi bocznej.
Czy chodzi tutaj o trójką BDE?
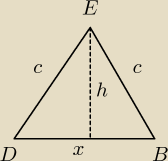 x = √a2+b2
a,b,c i h masz dane lub powinno się je jakos wyznaczyć
x = √a2+b2
a,b,c i h masz dane lub powinno się je jakos wyznaczyć
| H√a2+b2 | ||
No właśnie ja tak zrobiłem, wyszło mi P= | i źle, bo to nie ten trójkąt | |
| 2 |
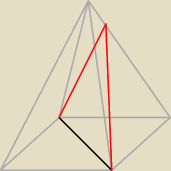 O ten Δ chodzi.
O ten Δ chodzi.

 .
.
| 1 | ||
wynosi | √a2+b2 ... stąd wniosek ... że ów płaszczyzna przecina CE w punkcie dla | |
| 2 |
| 1 | ||
którego odległość (w linii prostej) pomiędzy AE i CE wynosi właśnie | √a2+b2 | |
| 2 |
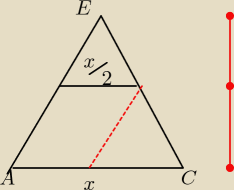 układasz proporcję (tw talesa)
układasz proporcję (tw talesa)
| 4H2+x2 | ||
P=√a2+b2*√ |  | |
| 16 |