trójkąt ABC jest równoboczny. Pomóż: W trójkąt równoramienny ABC wpisano koło. następnie poprowadzono dwie proste równoległe do podstawy: prostą l styczną do koła i prostą k, przechodzącą przez środek koła. proste te podzieliły trójkąt na trzy figury, których pola pozostają w stosunku 1:3:5(licząc od pola trójkąta). wykaż, że trójkąt ABC jest równoboczny.

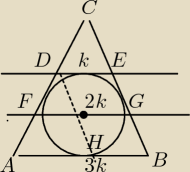
AS: PCDE : PDEFG : PFGAB = 1 : 3 : 5 czyli PCDE : PCFG : CAB = 1 : 4 : 9 Trójkąty te są podobne , a pola ich są proporcjonalne do kwadratów odpowiednich boków.. Stąd DE = 1*k , FG = 2*k , AB = 3*k Czworokąt ABDE jest opisany na okręgu, co oznacza że sumy przeciwległych boków są równe AB + DE = AD + BE i AD = BE AD + AD = 3*k + k ⇒ 2*AD = 4*k ⇒ AD = 2*k Przesuńmy BE równolegle do D Otrzymamy wtedy trójkąt o wszystkich bokach równych AD = 2*k , DH = EB = 2*k , AH = AB − HB = 3*k − k = 2*k Ponieważ ΔABC jest podobny do ΔADH a ten jest równoboczny więc i ΔABC jest równoboczny c.n.d..

piotreko96: skąd sie bierze że HB = k ?

piotreko96: a już chyba wiem...równoległobok, no nie?

M:

Ewa: skąd wziął się stosunek pól poszczególnych trójkątów?