oblicz dlugosci bokow trojkata Pomóż: w trojkacie ostrokatnym ABC poprowadzono wysokosci CD i AE, ktore przeciely sie w punkcie F. pole trpjkata CFE jest cztery razy wieksze od pola trojkata ADF.Wiedzac, ze AF=5cm, FD=3cm,AD=4cm, oblicz dlugosci bokow trojkata.

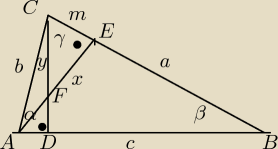
AS: Dane: AD = 4 , DF = 3 , AF = 5 , PΔCEF = 4*PΔADF Korzystam z wzoru na pole trójkąta: P = 0.5*a*b*sin(fi) gdzie fi jest kątem miedzy bokami 1. PΔCEF = 4*PΔADF 1/2*x*y*sin(fi) = 4*1/2*5*3*sin(fi) ⇒ x*y = 60 [1] równanie 1 2. ΔCEF jest podobny do ΔADF stąd proporcja x/y = 3/5 ⇒ 3*y = 5*x [2] równanie 2 3. Rozwiązuje układ równań [1] i [2] y = 5*x/3 x+5*x/3 = 60 ⇒ x² = 36 ⇒ x = 6 y = 5*6/3 = 10 4. ΔACE: AE = AF + FE = 5 + 6 = 11 , z tw.Pitagorasa: b² = CD² + AD² = 13² + 4² = 185 ⇒ b = √185 5. tg(α) = CD/AD = 13/4 stąd wyznaczymy α (z tablic) 6. sin(γ) = AE/AC = 11/√185 stąd wyznaczymy γ (z tablic) 7. β = 180 − (α + γ ) 8. z tw.sinusów: a/sin(α) = b/sin(β) ⇒ a = b*sin(α)/sin(β) c/sin(γ) = b/sin(β) ⇒ c = b*sin(γ)/sin(β)