oblicz stosunek pola Pomóż: W trojkacie prostokatnym jedna z przyprostokatnych jest dwa razy krotsza od przeciwprostokatnej. oblicz stosunek pola kola wpisanego w ten trojkat do pola kola opisanego na tym trojkacie.

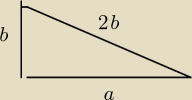
AS: 1. z tw.Pitagorasa: a² + b² = (2*b)² ⇒a² = 3*b² ⇒ a = b*√3 2. Promień koła opisanego na tr.prostokatnym = połowie przeciwprostokatnej. R = (2*b)/2 = b 3. Promień koła wpisanego w trójkąt r = PΔ/(połowa obwodu) r = (a*b/2)/(a + b + 2*b)/2 = a*b/(a + 3*b) r = b*√3*b/(b*√3 + 3*b) = b*√3/(3 + √3) 4. Stosunek pól kół k = π*r²/(π*R²) = r²/R² k = (b*√3/(3 + √3))²/b² = 3/(3 + √3)² = 3/(9 + 2*3*√3 + 3) k = 3/(12 + 6*p(3}) = 3/6*(2 + √3) = 1/2*(2 + √3) 5. Po zniesieniu niewymierności tj. po wymnożeniu licznika i mianownika przez 2 − √3 otrzymamy k = (2 − √3)/2

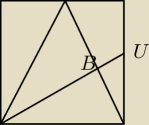
Anonimus: Wpisujemy w kwadrat linię łamaną, składającą się z 3 odcinków prostych. Każdy z nich łączy środek jednego boku z wierzchołkiem kwadratu, tak, jak pokazano na rysunku. Jaka jest długość całkowita linii łamanej, jeśli długość małego odcinka |BU| wynosi 1cm? Uzasadnij swoją odpowiedź.