 1.W płycie metalowej o powierzchni 136π cm2 należy wywiercić dwa większe i cztery mniejsze
otwory w kształcie koła tak aby średnice ich różniły się o 2cm, a suma pól wszystkich otworów
stanowiła czwartą część powierzchni płyty. Oblicz długość promieni otworów.
2.Dla nowo oddanej szkoły ponadgimnazjalnej zaprojektowano na boisko sportowe plac w kształcie
prostokąta. Aby jednak nie niszczyć zadrzewienia postanowiono zmniejszyć długość
projektowanego boiska o 30m a szerokość zwiększyć o 10m, otrzymując w ten sposób boisko
kwadratowe o polu stanowiącym 80% boiska zaprojektowanego pierwotnie. Oblicz długość boku
boiska po zmianach.
3.Absolwenci pewnej szkoły ponadgimnazjalnej, gratulując sobie zdania egzaminu maturalnego,
wymienili uściski dłoni. Wiedząc że podano sobie ręce aż 17955 razy, oblicz ilu absolwentów
zdało egzamin maturalny.
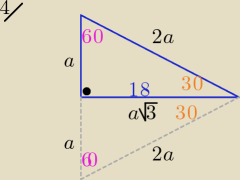
4.W trójkącie prostokątnym miara kąta ostrego jest równa 30 stopni. Wiedząc że długość dłuższej
przyprostokątnej jest równa 18cm, oblicz długości pozostałych boków trójkąta, nie korzystając
z funkcji trygonometrycznych.
Byłbym wam bardzo wdzięczny za pomoc
1.W płycie metalowej o powierzchni 136π cm2 należy wywiercić dwa większe i cztery mniejsze
otwory w kształcie koła tak aby średnice ich różniły się o 2cm, a suma pól wszystkich otworów
stanowiła czwartą część powierzchni płyty. Oblicz długość promieni otworów.
2.Dla nowo oddanej szkoły ponadgimnazjalnej zaprojektowano na boisko sportowe plac w kształcie
prostokąta. Aby jednak nie niszczyć zadrzewienia postanowiono zmniejszyć długość
projektowanego boiska o 30m a szerokość zwiększyć o 10m, otrzymując w ten sposób boisko
kwadratowe o polu stanowiącym 80% boiska zaprojektowanego pierwotnie. Oblicz długość boku
boiska po zmianach.
3.Absolwenci pewnej szkoły ponadgimnazjalnej, gratulując sobie zdania egzaminu maturalnego,
wymienili uściski dłoni. Wiedząc że podano sobie ręce aż 17955 razy, oblicz ilu absolwentów
zdało egzamin maturalny.
4.W trójkącie prostokątnym miara kąta ostrego jest równa 30 stopni. Wiedząc że długość dłuższej
przyprostokątnej jest równa 18cm, oblicz długości pozostałych boków trójkąta, nie korzystając
z funkcji trygonometrycznych.
Byłbym wam bardzo wdzięczny za pomoc 

| 18 | ||
4/ a√3= 18 ⇒ a= | = 6√3 | |
| √3 |

| −2−14 | ||
R1= | <0 odrzucamy | |
| 2*3 |
| −2+14 | ||
R2= | = 2 | |
| 2*3 |