matematykaszkolna.pl
Calka. O.: Oblicz pola figur ograniczonych liniami− wykresami funkcji f(x)=x2 oraz f(x)=√x
3 gru 20:21
Krzysiek: obszar całkowania: http://www.wolframalpha.com/input/?t=crmtb01&f=ob&i=y%3Dx%5E2%20%2Cy%3Dsqrt(x) spróbuj określić granice całkowania.
3 gru 20:22
O.: jakaś podpowiedź...?
3 gru 20:34
O.: granice całkowania...?
3 gru 20:41
Krzysiek: na rysunku jest wszystko.. x∊[0,1] na tym przedziale y=√x osiąga większe wartości od y=x2 zatem pole tej figury to: ∫01 (√x−x2)dx
3 gru 20:43
O.:
1 
?
3 
3 gru 21:01
O.: ponawiam i proszę o sprawdzenie emotka
3 gru 21:13
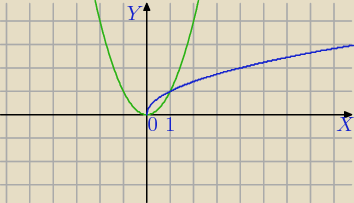
Mila: rysunekf(x)=x2 oraz f(x)=√x ;x≥0 Granice całkowania : x2=√x /2 ; x4=x⇔x4−x=0 x(x3−1)=0 x=0 lub x=1 ( możesz też odczytać i sprawdzić) 0∫1(√x−x2)dx dokończ
 1 
wynik
 3 
3 gru 21:17
O.: dokonczylam samodzielnie na karteluszce i wynik sie zgodzil emotka dzieki emotka
3 gru 21:20
O.: a taki przykladzik − to samo polecenie tylko linie ograniczajace to f(x)=lnx, oś OX i prosta x=e zaczęlam tak x∊[1,e] i stad e ∫(lnx−x)=... 1 dobrze kombinuje? emotka
3 gru 21:23
O.: ponawiam emotka
3 gru 21:34
Krzysiek: krzywa ograniczająca figurę od dołu to: y=0 więc powinno być: ∫1e (lnx−0)dx
3 gru 21:39
Mila: 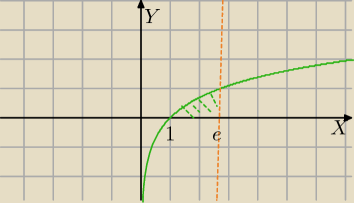rysunek1∫e(lnx−0)dx oś OX ma równanie y=0
3 gru 21:43
O.: wyszlo 1?
3 gru 21:49
O.: i ostatni przyklad −to samo pol ale linie ogr to f(x)=cosx os OX os OY oraz prosta x= π
3 gru 21:55
O.: emotka
3 gru 22:07
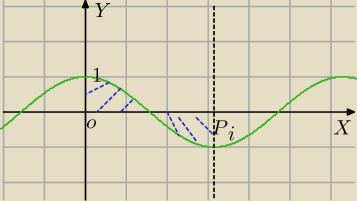
Mila: rysunekP=2*0∫π/2cosxdx
3 gru 22:11