Równania kwadratowe kosmita23: Między dwoma drzewami oddalonymi od siebie o 20 m rozwieszono poziomo sznur− napięty. Po rozwieszeniu prania sznur ten przyjął kształt paraboli. Wyznacz równanie tej paraboli w wybranym układnie współrzędnych, wiedząc że w najbliższym punkcie sznur był pół metra niżej od początkowego położenia. Prosze o pomoc nei wiem jak za to sie zabrać,umiem liczyć równania kwadratowe delta itd. ale z tym zadaniem mam ogromny problem.

Mati_gg9225535: w najblizszym punkcie czy najniższym ?

kosmita23: najniższym przepraszam

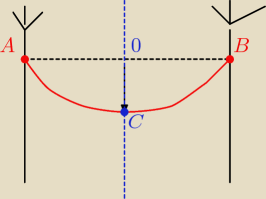
MQ: A=(−10;0) B=(10;0) C=(0; 0,5) y=ax²+bx+c Podstawiasz te trzy punkty do równania i dostajesz układ równań na a, b, c albo wysilasz wyobraźnię i z równania kanonicznego.

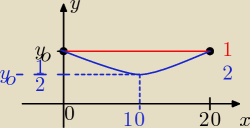
Mati_gg9225535: no wiec tak: rysunek wszystko Ci powie masz uklad trzech równań: f(x) = ax² + bx + c postan ogolna f(0) = y₀ f(20) = y₀

	1
f(10) = y0 −
	2

podstaw do postaci ogolnej i wylicz a b i c

kosmita23: ale jak mam to podstawić co jest moim a co b a co c zebym potem mógł wyliczyć x1,x2 deltę

MQ: W moim przypadku nie liczysz żadnej Δ Podstawiasz pierwszą wsp. punktu za x do równania. Drugą wsp. za y do równania. I dostajesz trzy równania na a, b i c. Po prostu prosty układ równań. Nie masz liczyć x₁ i x₂, tylko wyznaczyć równanie paraboli, czyli wyliczyć jej współczynniki −− właśnie a, b i c.