całki
ignis: Mam taki przykład:
Wyznacz pole ograniczone krzywymi:
y=x2+2x y=3
Uroki całek:−/ Ma ktoś jakis pomysł jak sie do tego zabrac?
24 maj 21:11
Edek: yyy...
a czasem tam niema czegoś takiego y≥x
2=2x oraz y≤3 czy czoś podobengo

24 maj 21:36
ignis: no własnie nie, ma być dokładnie tak jak napisałam powyżej. Nie wychodzi mi nawet szkic
szukanego pola ;−(
25 maj 09:03
Andrzej: no ja mam pomysł, obsuń tą parabolę o 3 w dół, wtedy będziesz musiał policzyć pole identycznego
obszaru tylko już ograniczonego parabolą i osią OX, czyli zwykłą całkę. A ponieważ ten obszar
będzie pod osią, to musi być minus ta całka. Powinna Ci wyjść minus całka od−3 to 1 z funkcji
x2+2x−3. Poradzisz już sobie ?
25 maj 09:21
Bogdan:
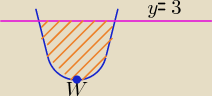
Wierzchołek paraboli W = (−1, −1)
25 maj 09:29
ignis: Prosze o jakieś wskazówki, Punktami przecięcia sie paraboli sa 1 i −3? jak dokladnie bedzie
wygladał wzór na pole?
25 maj 09:35
ignis: tak mi wyszła dzieki
25 maj 09:35
ignis: P=∫1 −3(x2+2x)−3)dx
25 maj 09:40
Bogdan:
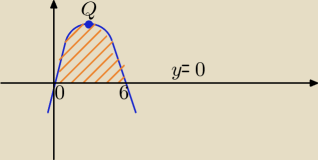
Warto rozpatrzeć obszar zawarty między parabolą y = −x
2 + 6x mającą wierzchek Q(3, 9)
i prostą y = 0, czyli osią x.
6
Pole tego obszaru P = ∫ (−x
2 + 6x) dx
0
25 maj 09:51
ignis: Przepraszam ale za nic nie moge dojść dlaczego −x2+6x ?i punkty przecięcia sie 0 i 6? mi
wychodza inne
25 maj 10:21
Bogdan:
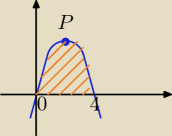
Czy łatwiej jest wyznaczyć pole ograniczone krzywymi y = x
2 + 2x i y = 3, czy też pole
ograniczone krzywymi y = −x
2 + 6x i y = 0 ?
To teraz analogicznie do paraboli y = −x
2 + 6x zbuduj parabolę odpowiadającą sytuacji
z Twojego zadania i podaj zapis pola stosując całkę oznaczoną. Załączam szkic.
25 maj 11:14

 Wierzchołek paraboli W = (−1, −1)
Wierzchołek paraboli W = (−1, −1)
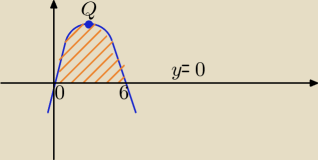 Warto rozpatrzeć obszar zawarty między parabolą y = −x2 + 6x mającą wierzchek Q(3, 9)
i prostą y = 0, czyli osią x.
6
Pole tego obszaru P = ∫ (−x2 + 6x) dx
0
Warto rozpatrzeć obszar zawarty między parabolą y = −x2 + 6x mającą wierzchek Q(3, 9)
i prostą y = 0, czyli osią x.
6
Pole tego obszaru P = ∫ (−x2 + 6x) dx
0
 Czy łatwiej jest wyznaczyć pole ograniczone krzywymi y = x2 + 2x i y = 3, czy też pole
ograniczone krzywymi y = −x2 + 6x i y = 0 ?
To teraz analogicznie do paraboli y = −x2 + 6x zbuduj parabolę odpowiadającą sytuacji
z Twojego zadania i podaj zapis pola stosując całkę oznaczoną. Załączam szkic.
Czy łatwiej jest wyznaczyć pole ograniczone krzywymi y = x2 + 2x i y = 3, czy też pole
ograniczone krzywymi y = −x2 + 6x i y = 0 ?
To teraz analogicznie do paraboli y = −x2 + 6x zbuduj parabolę odpowiadającą sytuacji
z Twojego zadania i podaj zapis pola stosując całkę oznaczoną. Załączam szkic.