yyyy pomysl
MarcinekzBogdanca: Pomoże ktoś ?
P(A'uB') obliczyć jeśli . P(A\B)=14 P(B\A)= 13 a AuB jest zdarzeniem przeciwnym
3 gru 18:34
Marcinek: I jak pomoże ktoś ?

3 gru 20:25
Bogdan:
A∪B jest zdarzeniem przeciwnym do którego zdarzenia?
3 gru 21:13
ketonal: Ooo nie nie jest to zdarzenie PEWNE przepraszam blad jakis sie wkradl.
3 gru 21:26
ketonal: Z telefonu teraz jak cos dlatego inna nazwa, ale to ciagle ja

3 gru 21:48
Bogdan:
Czy A∪B jest zdarzeniem pewnym?
3 gru 21:55
ketonal: Tak
3 gru 21:55
Bogdan:
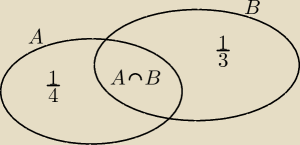
| | 1 | | 1 | |
P(A∪B) = 1 ⇒ |
| + P(A∩B) + |
| = 1 |
| | 4 | | 3 | |
P(A'∪B') = ...
3 gru 22:13
3 gru 22:22
Bogdan:
| | 5 | |
Czego dotyczy liczba |
| , którą podałeś? Nie jest to jednak P(A'∪B') |
| | 12 | |
3 gru 22:26
ketonal: Jak nie to juz kurde nie mam pomyslow .
3 gru 22:30
ketonal: Nasunela mi sie jeszcze odpowiedz ze to moze 0 poprostu czyli zbior pusty
3 gru 22:33
Bogdan:
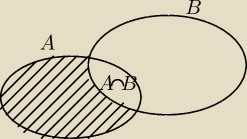
Jeśli P(A∪B) = 1, to część zakreskowana oprócz P(A\B) czym jest?,
(rozpatrz wszystkie możliwości), analogicznie po drugiej stronie (nie chciało mi się kreskować)
3 gru 22:43
ketonal:
A zakreskowane toP(A)−PAiloczynB
3 gru 22:50


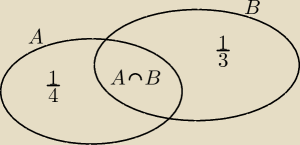
 Jeśli P(A∪B) = 1, to część zakreskowana oprócz P(A\B) czym jest?,
(rozpatrz wszystkie możliwości), analogicznie po drugiej stronie (nie chciało mi się kreskować)
Jeśli P(A∪B) = 1, to część zakreskowana oprócz P(A\B) czym jest?,
(rozpatrz wszystkie możliwości), analogicznie po drugiej stronie (nie chciało mi się kreskować)