oblicz objętość
Majka: Sześcian o krawędzi równej 6 przecięto płaszczyzną przechodzącą przez trzy jego wierzchołki
i nie zawierającą żadnych krawędzi. Oblicz objętość mniejszej, odciętej części.
2 gru 21:47
Kate: mniejszą odciętą częścią jest ostrosłup o podstawie trójkąta równobocznego − krawędź podstawy
(bok trójkąta) to przekątna ściany sześcianu, a krawędzie boczne ostrosłupa są krawędziami
sześcianu....
2 gru 21:50
Majka: wyjdzie 1/6 * 63 czyli 36?
2 gru 21:52
Kate:
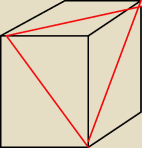
2 gru 21:53
Kate: wysokość ostrosłupa 2
√3
a objętość − 36
2 gru 21:58
Majka: a tak w woli ścisłości mogłabyś zapisać mi obliczenia
Chcę mieć pewność, że mam dobrze zrobione.
2 gru 22:03
Kate: | | 6√2√3 | |
wysokość postawy (tr.równobocznego):h= |
| |
| | 2 | |
i teraz U[2}{3} *h=2
√6
z Pitagorasa: (2
√6)
2+H
2=6
2
stąd H=2
√3
| | 1 | | (6√2)2√3 | |
V= |
| * |
| *2√3=36 |
| | 3 | | 4 | |
2 gru 22:10
2 gru 22:11
Kate:
2 gru 22:11
Aga1.: Każdy trójkąt może być podstawą.
Najprościej
2 gru 22:15
Majka: ja to zrobiłam na początku tak jak Aga1.
2 gru 22:19
Majka: właściwie wynik wychodzi ten sam, czyli obojętnie którym sposobem to zrobię?
2 gru 22:20
Aga1.: Oczywiście, że każdy sposób jest dobry, tylko niektórzy wybiorą prostszy.
2 gru 22:24
Bogdan:
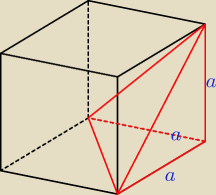
A może tak jest najprościej
| | 1 | | 1 | | 1 | |
V = |
| * |
| a2 * a = |
| a3 |
| | 3 | | 2 | | 6 | |
2 gru 22:31
Kate: ofkors że najprościej...
czasem wystarczy inaczej spojrzeć a ja tym razem spojrzałam zbyt krzywo....
2 gru 22:40
hakelbery: który odcinek jest tutaj właściwie wysokością ?
24 mar 11:15
irena_1:
U Bogdana− pionowa (czerwona) krawędź sześcianu
24 mar 12:35