system bcd i szesnastkowy szymek: Liczbę (0110 0101 0011 0111)BCD przedstawić w systemie szensastkowym HELP JAKI byl na to sposob

Andrew: http://blue_rider_hp.republika.pl/articles/tekst/liczby.html

Sławek: 0110 0101 0011 0111_BCD → 6537₁₀ 6537₁₀ → 1989₁₆

szymek: pytanie, jak zrobiles z dziesietnego na szensastkowy?

Student: 0110 8421 1 − prawda 4+2 daje 6 stąd 6 w 1 argumencie wyniku dalej: 0101 8421 4+1=5 65..... wynik

Sławek: Dzieląc (dzielenie z resztą) liczbę dziesiętną prze podstawę systemu na który chcesz zamienić, czyli 16. Otrzymane reszty zapisujesz w odwrotnej kolejności i masz zapis w systemie szesnastkowym. Pamiętaj, że jak otrzymasz reszty większe od 9 to w zapisie końcowym zamiast 10 piszesz A, 11 − B, 12 − C, itd. aż do 15 − F.

szymek: moglbys to pokazac na tym przykladzie? bo troche nie rozumiem, dziele 6 przez 16 i tu ma mi reszta wyjsc? albo 65? wtedy reszta wychodzi 1 a nie jak, powinna czyli 9 w odwroconej polejnosci.

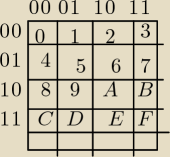
Mateusz: Prosta tabelka wystarczy zapamietac schemat jej tworzenia np w szesnastkowym F_(D)=1111

szymek: Mateusz, to ze odczytam sobie ze 0110 to 6, 0101 to 5, 0011 to 3 i 0111 to 7 nie czyni z liczb 6537 juz szestnastkowego prawda? tylko dziesietny?

asdf: przeczytaj trochę o kodzie BCD to przyznasz rację

Mateusz: No tak nie dopatrzyłem ze masz tam BCD

Sławek: 6537:16 = 408 r 9 408:16 = 25 r 8 25:16 = 1 r 9 1:16=0 r 1 Reszty przepisane w odwrotnej kolejności :1989

szymek: w ten sposób! dzieki wielkie ciekawe tylko ile zajmie mi wyliczenie tego skoro na kolosie nie moge kalkulatora uzywac chyba pod kreska bd musial

asdf: 0110 0101 0011 0111_BCD = 6537₁₀= 1989₁₆ tak mi wychodzi

asdf: @szymek powinieneś móc używać tego na kolosie, a jak nie to dadzą Ci prostsze liczby. Ja kodowanie liczb zaliczyłem to i Ty zaliczysz (10/10)

Mateusz: szymek skorzystaj z rady asdf jesli nie chcesz długo liczyc

szymek: że niby mam uzyc kalkulatora? yhh to by bylo... nielegalne...^^ tak wogole moge tu jeszcze uzyskac porady co do tematu minimalizacji fukncji bo mam niewielka szczegolowa zagwostke? to niby jeszcze elementy matmy szeroko pojętej

asdf: jakiej funkcji, chodzi Ci o algebre boolowską?

szymek: coś takiego Zminimalizować względem jedynek funkcję (a,b,c,d)=Π(0,2,6,8,10,13,(4,12,15)) chodzi mi o znak Π, jak nam na cwiczeniach dawali funkcje z tym znakiem to minimalizowalismy ją po zerach, rozumiem wtedy ze musze sobie wypisac funkcje f(abcd)∑ i bedzie ona zawierala liczby (czy tez argumenty) ktorych nie ma przy Π, np. 1,3,4,5, tylko nie wiem gdzie to ma swoj kres, tzn moglbym rownie dobrze wziasc pod uwage liczbe 16, ktora do Π nie nalezy

Sławek: Możesz zapamiętać kolejne potęgi liczby 16 i będzie łatwiej. 16³=4096 16²=256 16¹=16 16⁰=1 Będą to wagi kolejnych pozycji poz. 3 2 1 0 waga 4096 256 16 1

asdf: jaką liczbę 16?! liczbę 16 nie zapiszesz na 4 bitach. Robiliście to tablicą Karnaugh czy implikantami prostymi?

Sławek: Nie, bo jak masz funkcję 4 argumentów to zakres liczb będzie od 0 do 15.

szymek: i tym i tym, ale na kole beda tablice karnaugh wiec tym jakbys mogl przetlumaczyc

szymek: aaaa, wiec dla 5 zmiennych jest 32, to wypisalbym przykladowo (a,b,c,d,e)=Π(0,2,6,8,10,13,(4,12,15)) f∑ (1,3,,5,7,9,11,14 i wszystkie dla 16+ do 32?)

asdf: no to jedziesz z tablicy karnaugh, wiesz jak się łączy itd?

szymek: tak, minimalizacje umiem

Sławek: Trochę pomieszałeś nie wszystkie − chyba, że autor zadania tak poda Taki zapis f(a,b,c,d)=Π [0,2,6,8,10,13,(4,12,15)] jest równoważny takiemu f(a,b,c,d)=∑[1,3,5,7,9,11,14,(4,12,15)]

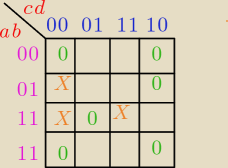
asdf: taka Ci wychodzi tablica?

szymek: tak

asdf: łączysz jedynki ( puste pola) czy zera?

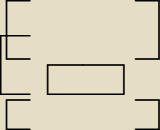
szymek: i tak bym to minimalizowal

szymek: aa po jedynkach to odwrotnie oczywiscie tam gdzie puste pole byly by 1−nki i bym minimalizowal

asdf: _{ad + d + abc = neguję = (a + d})_d(_{a + b + c)}

asdf: robiłem to z jedynek, też Ci tak wyszło?

szymek: yy to znaczy zminimalizowales 1nki i znegowales czy na odwrot? po zerach i negacja?

asdf: łączenei jedynek napisałem, później negacja (przechodzenie dodawania w mnożenie i na odwrót)

asdf: Z resztą masz treść zadania: Zminimalizować względem jedynek funkcję (a,b,c,d)=Π(0,2,6,8,10,13,(4,12,15))

Sławek: a'd+b'd+abc ((a'd+b'd+abc)')'=((a'd)'(b'd)'(abc)')'

asdf: heh Są różne formy, ale moja chyba jest bardziej zminimalizowana, nie będę sprawdzać Twojego, ani swojego też już nie − basha mam na głowie