Wyznacz zbiór rozwiązań
Arek: wyznacz zbiór rozwiązań:
a) równania sin2x−sinx=0
b)nierówności sin2x>sinx w przedziale <0,2π>.
rozwiązanie proste sinx(2cos−1)=0
sinx(2cos−1)
ale wyjaśni mi ktoś jak z tym przedziałem sobie poradzić ?
2 gru 19:37
krystek: | | 1 | |
sinx=0 lub cosx= |
| i wybierasz tylko te kąty mieszczące się w podanym przedziale |
| | 2 | |
2 gru 19:39
Arek: a mógłbyś rozpisać ? Tyle to wiem to co napisałeś
2 gru 19:48
Bogdan:
a) odpowiedź jest wprost: sin2x = sinx ⇒ 2x = x + k*2 lub 2x = π − x + k*2π
2 gru 19:50
krystek: | | π | | π | |
x=0+kπ lub x= |
| +2kπ lub x=(2π− |
| )+2kπ i wybieraj |
| | 3 | | 3 | |
| | π | |
stąd x=0,π,2π, lub x= |
| lubx= . wylicz ostatni |
| | 3 | |
2 gru 19:52
Arek: no 5/3 pi
no spoko a w nierówności jak to będzie wyglądać ?
2 gru 20:00
krystek: to było do równania
Do nierówności zwróć uwagę na zapis Bogdana
Wykres tych dwóch funkcjii zobacz gdzie sin2x>sinx
2 gru 20:05
Arek: aaa czyli rysuje i mam, dzięki
2 gru 20:06
Bogdan:
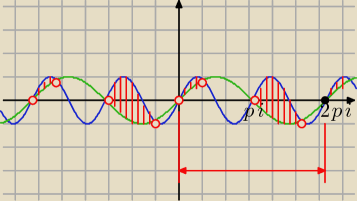
y = sin2x (niebieski wykres
y = sinx (zielony wykres)
sin2x = sinx ⇒ 2x = x + k*2π lub 2x = π − x + k*2π
| | π | | 2 | |
x = k*2π lub x = |
| + k* |
| π |
| | 3 | | 3 | |
| | π | | 5 | |
Dla x∊<0, 2π> sin2x > sinx ⇒ x∊(0, |
| )∪(π, |
| π) |
| | 3 | | 3 | |
2 gru 20:08
krystek: @
Bogdan 
2 gru 20:09
Bogdan:
2 gru 20:14