Basia:
pierwiastki będą rzeczywiste ⇔ Δ = 4a
2−4b = 4(a
2−b)≥0 ⇔ a
2−b ≥ 0 ⇔ a
2≥b
co jest prawdą dla każdego b≤0 i dla tych b>0, dla których punkty (a,b) leżą na lub poniżej
paraboli
b = a
2
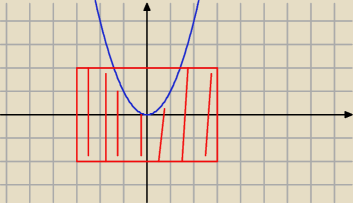
jeżeli k, l >0 to daje prostokąt o bokach 2k, l (pod osią OX)
obszar nad osią OX będzie zależał od tego jakie są k i l
trzeba rozważyć dwa przypadki:
1. k
2>l (jak na rysunku)
wtedy mamy dwa prostokąty o bokach k−
√l, k + 2
0∫
√l x
2dx
2. k
2≤l
wtedy mamy 2
0∫
kx
2dx
jeżeli nie było założenia, że k,l>0 trzeba tam wszędzie wstawić wartość bezwzględną
 pierwiastki będą rzeczywiste ⇔ Δ = 4a2−4b = 4(a2−b)≥0 ⇔ a2−b ≥ 0 ⇔ a2≥b
co jest prawdą dla każdego b≤0 i dla tych b>0, dla których punkty (a,b) leżą na lub poniżej
paraboli
b = a2
jeżeli k, l >0 to daje prostokąt o bokach 2k, l (pod osią OX)
obszar nad osią OX będzie zależał od tego jakie są k i l
trzeba rozważyć dwa przypadki:
1. k2>l (jak na rysunku)
wtedy mamy dwa prostokąty o bokach k−√l, k + 20∫√l x2dx
2. k2≤l
wtedy mamy 20∫kx2dx
jeżeli nie było założenia, że k,l>0 trzeba tam wszędzie wstawić wartość bezwzględną
pierwiastki będą rzeczywiste ⇔ Δ = 4a2−4b = 4(a2−b)≥0 ⇔ a2−b ≥ 0 ⇔ a2≥b
co jest prawdą dla każdego b≤0 i dla tych b>0, dla których punkty (a,b) leżą na lub poniżej
paraboli
b = a2
jeżeli k, l >0 to daje prostokąt o bokach 2k, l (pod osią OX)
obszar nad osią OX będzie zależał od tego jakie są k i l
trzeba rozważyć dwa przypadki:
1. k2>l (jak na rysunku)
wtedy mamy dwa prostokąty o bokach k−√l, k + 20∫√l x2dx
2. k2≤l
wtedy mamy 20∫kx2dx
jeżeli nie było założenia, że k,l>0 trzeba tam wszędzie wstawić wartość bezwzględną