zadanie funkcja adaś: http://www.matematyka.pl/69298.htm jak dojść do wyniku mając:

⎧	x1−2 +x2−2>0
⎩	(x1−2)(x2−2)>0

ZKS:

	c
{x1 + x2 > 4 ⇒		− 4 > 0
	a

	c		−b
{x1x2 − 2(x1 + x2) + 4 > 0 ⇒		− 2		+ 4 > 0
	a		a

adaś: dzięki Tobie bardzo, mógłbyś mi jeszcze co nieco powiedzieć co dalej mam czynić bo dopiero takie coś zaczynam

ZKS: Znasz wzory Viete'a?

adaś: widziałem je tylko, ale nie wiem jeszcze za bardzo co z tym zrobić , powiesz ? Wyznaczyć a i podstawiać?

ZKS: f(x) = ax² + bx + c jeżeli b² − 4ac ≥ 0 to wtedy

	−b
x1 + x2 =
	a

	c
x1x2 =
	a

Przykładowo f(x) = x² − 4x + 3 Δ = 16 − 12 = 4 > 0

	−(−4)
x1 + x2 =		= 4
	1

	3
x1x2 =		= 3
	1

adaś: 1 gru 2012 23:03 ← co dalej ? Pokaż mi jak to robisz proszę

Krzysiek : Zas duzo pisania . maly szczegol ale 1 12 o godz 23,03 ZKS sie pomylil i napisal ze

	c		−b
x1+x2=		ma byc =		Adas ale juz tam gdzie pokazal CI jak zastosowac te wzory to
	a		a

napisal dobrze . Wez to pod uwage i nie rob zadymy Jezeli wyjdzie z rownania Δ≥0 czyli wieksza badz rowna 0 to rownanie posiada 2 pierwiastki czyli miejsca zrowe . Jest tez badz rowna zero dlatego ze jest pierwiastek ale podwojny czyli defakto tez dwa . W zadaniu masz napisane dla jakiego parametru m funkcja y=x²+mx+9 ma dwa pierwiastki wieksze od 2 Jesli funkcja ma miec dwa pierwiastki to Δmusi byc ≥0 Popatrz na funkcje i masz ze a=1 b=m bo przy x stoi m i c=9 to liczymy delte Δ=b²−4a*c≥0 to m²−4*1*9≥0 to m²−36≥0 to narusuj sobie ta parabole i zobaczysz ze m∊(−∞ −6>∪<6,∞) Masz juz 1 warunek jaki to musi byc parametr m Teraz ZKS to CI napisal ze jesli Δ≥0 to mozesz zastosowac wzory Viet'a . Rozbrajasz mnie tym ze napisales ze tylko je widziales . TY je miales znac albo w 1 albo w 2 klasie . A teraz jestes w ktorej ? CO mowia nam wzory vieta

	−b
1. suma miejsc zerowych (czyli pierwiastkow rownania ) czyli x1+x2=
	a

	c
2. Iloczyn miejsc zerowych czyli x1*x2=		Zobacz dokladnie tam gdzie ZKS podal CI
	a

przyklad jak policzyc i zrozum to. Majac wzory Vieta jestes w stanie okreslic jaki znak maja pierwiastki rownania bez liczenia tych pierwiastkow i takze wyznaczyc te pierwiastki . Zobacz np jesli iloczyn czyli x₁*x₂=3 (ten przyklad ZKS) to juz wiesz ze dwa pierwiaski maja ten sam znak albo sa dodatnie albo ujemne bo iiloczn dwoch liczb ujemnych tez jest dodatni . Tego na razie nie wiemy . Jak policzymy sume tych pierwiastkow czyli X₁+x₂=4 to widzimy ze suma jest dodatnia wobec tego te dwa pierwiastki musza byc dodatnie To teraz wiemy jaki znak maja te pierwiastki rownania tego co podal CI ZKS czyli x²−4x+3 to teraz mozemy wyznaczyc te pierwiastki , Iloczy ma byc rowny 3 . Iloczyn jakich liczb jest rowny 3 i maja byc dodatnie . Beda to liczby 1 i 3 bo 1*3=3 czyli x₁=1 i x₂=3 Teraz suma tych pierwiastkow ma sie rownac 4 to x₁+x₂=4 dodajemy i mamy 1+3=4 czyli sie zgadza . mamy tez wyznaczone pierwiastki bez ich liczenia tylko stosujac wzory VIeta . WIdzisz jak one sa przydatne ? ZA chwile wrocimy do dalszej czesci tego zadania a mianowicie zastosujemy te wzory Vieta .

Krzysiek : Teraz wracamy do naszej funkcji czyli f(x)=x²+mx+9 Pierwszy warunek ze funkcja posiada dwa pierwiastki vczyli Δ≥0 mamy juz wyznnaczony bo m∊(−∞,−6>∪<6,∞) Teraz jesli te pierwiastki (miejsca zerowe) maja byc wieksze od 2 to oznacza ze maja byc >0 czyli maja byc dodatnie .A co wiemy juz o pierwiastkach rownania jesli sa dodatnie Wiemy to ze ich suma jest tez dodatnia czyli >0 Teraz te pierwiasktki maja byc >2 to x₁>2 czyli x₁−2>0 a takze x₂>2 to x₂−2>0 To piszemy ze

	−b
x1−2+x2−2>0 czyli x1+x2−4>0 CVzemu rowna sie x1+x2 . ze wzorow Vieta =		. Zobacz
	a

	−b
w poscie tam napisalem czemu rowna sie a ,b ,c tej funkcji To mozemy zapisac ze		−4>0
	a

to −m−4>0 to −m>4 to m<−4 (zmieniam zwrot nierownosci bo mnoze przez liczbe ujemna (−1) to m∊(−∞,−4) bo ma byc mniejsze od −4 . Czyli z sumy pierwiastkow mamy wyznaczony drugi przedzial dla parametru m gdzie jesli podstawimy liczbe z tego przedzialu to funkcja bedzie miala dwa pierwiaski wieksze od 2 Jeszce cos wiadomo o pierwiastkach (miejscach zeowych funkcji ) jesli maja byc one dodatnie . Wiemy to ze iloczyn tych pierwiastkow musi byc >0 czyli (x₁−2)*(x₂−2)>0 to powinienes sobie sam to wymnozyc bo to nie jest trudne ale CI rozpisze x₁*x₂−2*x₁−2*x₂+4>0 Masz x₁*x₂ teraz dla −2x₁−2x₂ wyciagasz 2przed nawias i i bedzie x₁*x₂−2(x₁+x₂)+4>0 Teraz dobrze sie przypatrz tej nierownosci Mamy tutaj x₁*x₂ Czemu to sie rowna ? .Ze wzorow Vieta jest

	c
to iloczyn dwoch miejsc zerowycych i =		. W nawiasie masz tez x1+x2 to czemu to jest
	a

	−b
rowne JUz powinienes wiedziec ze to jest rowne ze wzoru Vieta		bo to suma dwoch
	a

	c		−b
miejsc zerowych Wiec zapiszmy ta nierownosc tak		−2*		+4>0 to
	a		a

9+2m+4>0 to 2 m>−13 to m>−6,5 czyli m∊(−6,5 ∞) czyli mamy wyznaczony trzeci warunek ze iloczyn tych pierwiastkow jest wiekszy od 0 dla m∊(−6,5 ∞) Teraz musisz polaczyc te 3 warunki czyli dla Δ≥0 m∊(−∞ −6>∪<6,∞) ze suma tych miejsc zerowych >0 dla m∊(−∞ −4) ze iloczyn tych miejsc zerowych >) dla m∊(−6,5 ,∞) i wyznaczyc czesc wspolna tych przedzialow. . TO juz sobie zrob i napisz do jakiego przedzialu bedzie nalezal parametr m . Czyli na osi liczbowej wyznaczysz . Nareszczie koniec.

Krzysiek : Naprawde wisisz flaszke .

krystek: Ty piszesz ,a czy to zainteresowany czyta ze zrozumieniem?

Krzysiek : Krystek. mam taka nadzieje ze chociaz troche z tego zrozumie i zda ta mature . Pozdrawiam .

adaś: nie musiałeś się tak rozpisywać chodziło mi tylko o rozwiązanie tego zadania sam bym doszedł później dlaczego itp. dzięki bardzo Dla mnie przedział czyli ta część wspólna będzie się zaczynała dla m∊ (−6,5; 6> , tylko czy na pewno nawias domknięty ?

Krzysiek : Adas Ty nie pisz ze nie musialem bo nie chcesz postawic flaszki .Nieladnie . Poza tym masz zle wyznaczony przedzial . Narysuj jeszce raz i zobacz dobrze gdzie te wszystkie razem 3 przedzialy sie pokrywaja Zobacz ze te 3 przedzialy sie pokrywaja w przedziale (−6,5 −6> bo w −6 bedzie kropka zamalowana

adaś: i tak Tobie wiszę nie tylko za to ,ale za inne pomoce

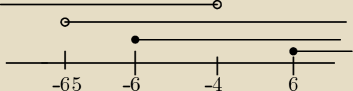
adaś: nie wiem czy dobrze narysowałem na osi liczbowej ,proszę o sprawdzenie

adaś: ?

adaś: Krzychu ,możesz to sprawdzić?

Krzysiek : Adas zle narysowales bo ma byc mniejsze od −6 bo masz przedzial (−∞,−6> a nie przedzial<−6 ∞) czyli od −6 w lewo a nie w prawo Poza tym tamte dobrze narysowane Popraw i narysuj

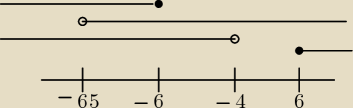
adaś: m∊ (−6,5;−6) nie bardzo jeszcze rozumiem tą szóstkę na plusie, ta szóstka się nie wlicza, część wspólna to po prostu to co łączy te "linie" jako całość w tym przypadku ?

adaś: sory m∊ (−6,5;−6>

Krzysiek : Nie wlicza sie to 6 do czesci wpspolnej bo to ma byc czesc wspolna wszystkich tych przedzialow . Wliczyl bys ta 6 wtedy gdy ten przedzial co jest (−∞ −4) by byl nie do −4 tylko np do10 Wtedy czyli idzie za 6 Czyli mamy przedzial m∊ (−∞ 10 ) taki Wiec narysuj te przedzialy czyli m∊(−∞ −6>∪<6,∞) m∊(−∞ 10) i m∊(−6,5,∞) . Zobacz ze teraz czesc wspolna tych wszystkich 3 przedzialow sie zmieni bo zobacz w ktorym miejscu sie pokrywaja te wszystkie przedzialy . Ano (−6,5,−6>∪<6 10) 6 jest lewostronnie domkniete bo 6 nalezy do wszystkich trzech przedzialow a 10 jest otwarte bo 10 nie nalezy do przedzialu m(−∞ 10) a wiec nie moze byc brane pod uwage do czesci wspolnej . Teraz narysuj te przedzialy A takze zrob rysunek i napisz jak bedzie czesc wspolna gdy przedzial m∊(−∞ 10 ) zamienisz na przedzial m∊(−∞10>

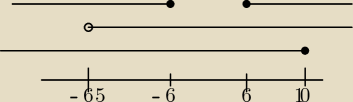
adaś: gdy go zmienię to będzie tak : (−6,5,−6>∪<6;10>

Krzysiek : Wiec tak . Adas dobrze i na zdrowie Jeszcze tak mysle ze powinienes na forum przeprosic ETE i poprosci ja o to zeby CI pomogla Mysle ze przeprosiny zostana przyjete .

adaś: Ok, więc Etko wybacz mi za moje głupiutkie zachowanie Jęśli tu wpadniesz na ten post, to proszę Cię abyś nadal mi pomagała

adaś: Krzychu zajrzyj tutaj proszę bo nie jestem pewnien czegoś→ https://matematykaszkolna.pl/forum/172129.html Ta oś liczbowa wzięła się z zadania: Szkicując odpowiedni wykres funkcji rozwiąz nierownosc: |x² − 6x| ≤ 2x odp. to niby x∊<4;8>∪{0} staram sobie narysować to na osi i wyznaczyć sumę

adaś: co ja muszę tutaj najpierw zrobić ? Miejsca zerowe x²−6x=0 x=0 x=6 ,potem x²−6x−2x≤0 x²−8x≤0 oraz −x²+6x−2x≤0 −x²+4x≤0 −x²≤−4x x²≥4x x²−4x≥0 dobrze robię?

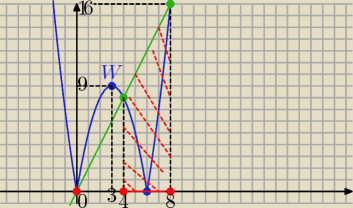
Eta: y= x²−6x −−− parabola W(3,−9) Niebieski wykres |x²−6x| część paraboli spod osi OX odbita nad oś OX W(3,9) miejsca zerowe x²−6x=0 ⇒ x(x−6)=0⇒ x=0 v x= 6 Zielony wykres y= 2x punkty wspólne prostej z wykresem niebieskim (0,0) i ( 8, 16) Rozwiązanie nierówności |x²−6x| ≤ 2x odczytujesz te "x" dla których wykres niebieski jest pod wykresem zielonym wraz z punktami wspólnymi' zatem odp: x∊<4, 8> U {0}

adaś: dzięki za rysunek teraz wiem dlaczego taka odpowiedz ,dzięki

Eta: @adaś Przez nieuwagą nie napisałam: Zielony wykres z wykresem niebieskim ma trzy punkty wspóne (0,0) i (8,16) i jeszcze (4,8)

Krzysiek : Adas. ja wracam teraz bardzo pozno z pracy. wiec nie zawsze bede o tak poznej porze czytal posty bo jestem juz zmeczony (przynjmniej ten tydzien ) . W poleceniu miales naszkicowac wykres i odczytac rozwiazania . Eta CI to ladnie narysowala i wytlumaczyla . takie wykresy paraboli czy to bedzie funkcja cala w module czy bedzie tylko jakis jej czynnik w wartosci bezwzglednej to juz miales tlumaczone jak rysowac Wiec pocwicz sobie jeszcze rysowanie . CHcialbym zebys postaral sie tez rozwiazac ta nierownosc algebraicznie . Tam z 03.12 0 godz23 04 dobrze zaczales rozwiazywac no ale nie wyznaczyles przedzialow Powinienes zaczac tak masz |x²−6x|≤2x teraz patrze dla jakich x to wyrazenie w module jest ≥0 wtedy opuszczajac modul nie znieniamy znaku (klania sie definicja wartoci bezwzglednej ) Wyznaczyles miejsca zerowe dla x²−6x czyli bedzie to x=0 i x=6 to teraz jesli masz miejsca zerowe wyznaczone to dla jakich x, x²−6x ≥0 zobacz jaka bedzie parabola . Dla Ciebie usniechnieta . to wtedy x∊(−∞ 0>∪<6,∞) przedzialy domkniete bo jest ≥0 Wiec dla x∊(−∞ 0>U<6,∞) nierownosc bedzie miala taka postac x²−6x≤2x to x²−6x−2x≤0 to x²−8x≤0 teraz patrzysz dla jakich x −ow ea funkcja x²−8x ≤0 rozlozmy to tak x(x−8)=0 to x=0 i x=8 i mamy jej miejsca zerowe . Treaz ta funkcja musi byc≤0 to jak narysujesz sobie wykres tej paraboli to zobaczysz ze ta funkcja x²−8x≤0 przyjmuje te wartosci w przedzialex∊ <0,8> Teraz musisz wyznaczyc czesc wspolna tych wszystkich przedzialow czyli x∊(−∞,0>U<6,∞) i x∊<0,8> . Teraz tak . ZObacz ze 0 nalezy zarowno do jednego jak i drugiego przedzialu wiec nalezy do czesci wspolnej i zapewne o to chodzilo CI w tych rysunkach (zawsze pisz o jakie zadanie chodzi ) Wiec czescia wspolna tych przedzialow jest {0} U<6,8> zero jest wziete w klamerke bo to jest punkt. Teraz patrzymy dla jakich x_ow x²−6x <0 wtedy opuszczajac wartosc bezwzglaedna zmienimy znak . Zobacz zetaq funkcja jest <0 w przedziale (0 ,6) czyli x∊(0,6) to dla tych x−ow |x²−6|≤2x zapiszemy −x²+6x≤2x to −x²+6x−2x≤0 wyznacz teraz przedzialy dla ktorych to funkcja jest ≤0 i wyznacz czesc wspolna tych przedzialow z przedzialem x∊(0,6) WIec jak juz to zrobisz to rozwiazaniem tej nierownosci bedzie suma przedzialow {0}U<6,8> i tego co CI wyjdzie . Wiec rozwiaz to na forum . W razie czego sie poprawi

adaś: Dziękuje Krzychu za jeszcze dokładniejsze wytłumaczenie

Agnieszka: x≥31x<11⇒x∊

Krzysiek : x∊(−∞,11)U<31,∞)

krystek: a gdy miedzy i to x∊{∅}