Trygonometria kąta ostrego Bobson:

	√3
Stosunek długości boków prostokąta wynosi		. Zatem cosinus kąta ostrego między
	3

	√2		√3		1		√3
przekątnymi prostokąta jest równy : A.		, B.		, C.		, D		.
	2		2		2		3

Proszę o pomoc

Mati_gg9225535: narysuj boki i przyjmij ze jeden jest równy √3 a drugi 3 z Tw. Pitagorasa policz przekątną i ułóż nowa f. trygonometryczna z przekątną mozesz przyjac ze te boki sa rowne tyle gdyz chodzi tylko o stosunek wiec spokojnie

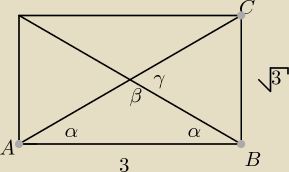Saizou : β=180−2α w ΔABC

	√3
tgα=		z tego wniosek że α=300 wówczas
	3

β=180−60=120 γ=180−120=60

	1
cos60=
	2

Bobson: czyli ten kąt gdzie się znajduje?

Bobson: ok dzięki już rozumiem