znalezienie błędu bolo: w czworokącie abcd wpisanym w okrąg dane są ad = 2, bc=10, cd=8, ab=4. Wyznacz miarę kąta między najkrótszmi bokami Obliczam z tw cosinusow, wszystko rozumiem i zgadzam się z odpowiedziami, "ale" z równania 2²+4²−2*2*4*cosα= 8²+10²−2*10*8*(cos 180 − α) obliczam α. Wychodzi −9/11 −> 35 stopni. Ale w odpowiedziach musze odjac jeszcze od 180 stopni moj wynik. Dlaczego, skoro wprowadzilem oznaczenia α i od poczatku nie liczylem juz β?

bolo:

Mila:

	−9
cosα=
	11

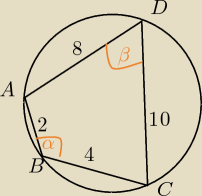
β≈35 cosα<0 to oznacza, że kąt jest rozwarty. α≈180⁰−35⁰≈145⁰