 DANE:
AC = 12
Z powodu iż PABC = PAEDC + PBDE = 96[cm2]
DANE:
AC = 12
Z powodu iż PABC = PAEDC + PBDE = 96[cm2]
| AC*AB | ||
PABC = | ||
| 2 |
| 12[cm] * AB | ||
96[cm2] = | ||
| 2 |
| BD | BE | DE | |||
= | = | = k (stosunek boków) | |||
| BA | BC | AC |
| 6 | |
= k2 (stosunek pól) | |
| 96 |
 Tak własnie w odpowiedziach jest.
Tak własnie w odpowiedziach jest. 
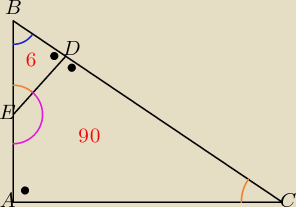
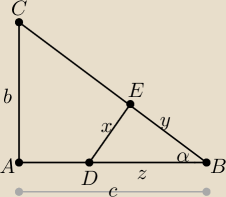
 W trójkącie prostokątnym ABC, α=90, przyprostokątna AC ma długość 12 cm. Odcinek DE,
prostopadły do przeciwprostokątnej BC, dzieli trójkąt na dwie figury o polach równych P1=6
cm2 i P2=90 cm2. Oblicz długości boków trójkąta DBE.
W trójkącie prostokątnym ABC, α=90, przyprostokątna AC ma długość 12 cm. Odcinek DE,
prostopadły do przeciwprostokątnej BC, dzieli trójkąt na dwie figury o polach równych P1=6
cm2 i P2=90 cm2. Oblicz długości boków trójkąta DBE.
 PABC = 90 + 6 = 96
PABC = 90 + 6 = 96
| PABC | 96 | ||
= k2 ⇒ | = 16 ⇒ k2 = 16 ⇒ k = 4, | ||
| PEBD | 6 |
| 1 | ||
b = 12, PABC = | *12*c ⇒ 6c = 96 ⇒ c = 16 | |
| 2 |
| b | |
= k ⇒ x = ... | |
| x |
| c | |
= k ⇒ y = ... | |
| y |