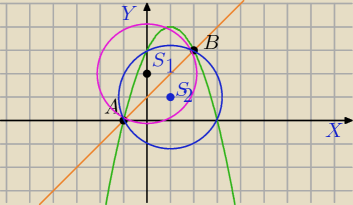
okręgi funkcja kamil : okręgi .....: Prosta k: y=x + 1 przecina parabolę o równaniu y=−x2 + 2x + 3 w punktach A i B. a) Oblicz wspólrzędne punktów A i B b) Napisz równanie okręgu o promieniu długości sqrt(5), jeśli odcinek AB jest cięciwą tego okręgu. c) Oblicz pole trójkąta ABS, gdzie S jest środkiem okręgu wyznaczonego w punkcie b). a) umiem, w b) wychodzą mi jakieś głupoty, czy dobry układ równań zrobiłem? (2−x)² +(3−y)²=(√5)² (−1−x)²+y²=(√5)²

Bizon: mając współrzędne punktów A i B (leżących na szukanym okręgu) i jego promień podstawiaj je do równania okręgu i policz z tego współrzędne środka

Mila: y=x + 1 przecina parabolę o równaniu y=−x² + 2x + 3 −x² + 2x + 3 =x+1 −x²+x+2=0 ⇔Δ x₁=−1 lub x₂=2 y₁=0 lub y₂=3 A=(−1,0) B=(2;3) S=(a;b) r=√5 (−1−a)²+b²=5 (2−a)²+(3−b)²=5⇔1+2a+a²+b²=4−4a+a²+9−6b+b²⇔ a+b=2 ⇔b=2−a podstawiamy do I równania (1+a)²+(2−a)²=5 po wykonaniu działań 2a²−2a=0 ⇔ a²−a=0 ⇔a(a−1)=0 a=0 i b=2 lub a=1 i b=1 S₁=(0;2) lub S₂=(1;1)

kamil : dziękuję bardzo! a wiesz może jak zrobić c ?

Mila: Obliczyć długość AB: |AB|=√3³+3²=√18=3√2 Odległość punktu S₁ od prostej AB to wysokość Δ. AB: y=x+1⇔x−y+1=0 S₁=(0,2)

	|1*0−1*2+1|		1
d=		=
	√12+12		√2

	√2
d=h=
	2

albo z tw. pitagorasa S₁A²=√1²+2² S₁A=√5 h²+(1,5√2)²=(√5)² h²=5−4,5

	√2
h=
	2

Teraz muszę zwolnić komputer, chyba sobie poradzisz

kamil : tak tak, dziękuję Ci bardzo, jesteś boska!