Romby Ela: Pole rombu, którego kąt rozwarty ma miarę trzy razy większą od miary kąta ostrego wynosi 16 cm2. oblicz długość boku rombu. (powinno wyjść 4 ⁴√2) Przekątne rombu mają długość 10 cm i 24 cm. oblicz sinus kąta ostrego tego rombu i na tej podstawie ustal, czy kąt ostry ma miarę większą czy mniejszą ok 45^o. ( odpowiedz: sin alfa = ¹²⁰₁₆₉, sin45^o = ^√2₂ alfa ∊(45^o, 90^o)) jak to zrobić ? Romb o długości 18 cm podzielono na trzy części o równych polach prostymi przechodzącymi przez wierzchołek kąta ostrego. Oblicz długość odcinków, na jakie te proste podzieliły boki. (6 cm, 12 cm) Bok kwadratu ABCD ma długość a. Na przeciwległych bokach AB i CD zbudowano trójkąty równoboczne, leżące wewnątrz kwadratu. Oblicz pole części wspólnej tych trójkątów. (^{(2√3−3)a2}₃) W romb, którego bok ma długość 5 cm, a kąt ostry ma miarę 60^o, wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu. (^75√3₁₆) Okrąg przechodzący przez wierzchołek kąta ostrego rombu i wierzchołki kątów rozwartych tego rombu dzieli przekątną rombu na dwa odcinki długości 17 cm i 8 cm. Oblicz pole rombu. (187,5)

tim: Pokazuję 1 i 4.

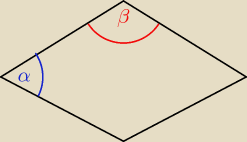
tim: Zad. 1. α = kąt ostry β = kąt rozwarty = 3α α + 3α = 180^O 4α = 180^O α = 45^O β = 135^O Korzystając z wzoru na pole rombu: P = a² * sin δ, gdzie a = bok, δ = kąt ostry rombu podstawiasz dane z zadania i liczysz. Wyjdzie ci taki wynik jak w odpowiedzi.

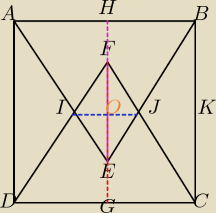
tim: Zad. 4. "Bok kwadratu ABCD ma długość a. Na przeciwległych bokach AB i CD zbudowano trójkąty równoboczne, leżące wewnątrz kwadratu. Oblicz pole części wspólnej tych trójkątów." Przyjmując oznaczenia jak na rysunku mamy: DANE: AB = BC = CD = AD = AE = EB = DF = FC = a

	1
AH = HB = DG = GC = BK = CK =		a
	2

FE = 2x IJ = 2y

	2x * 2y
Pole IEJF = Pole rombu o przekątnych FE, IJ =
	2

∡ BAE = 60^O (Korzystając z podobieństwa....) ∡ EIJ = 60^O ∡ FIJ = α= 60^O

	a√3
EH = GH = htrójkąta równobocznego o boku a =
	2

	a√3
HF = GE = BC − GF = a −
	2

	1		a√3		1		a√3
x = FO = OE = BK − HF =		a − (a −		) = −		a +
	2		2		2		2

2x = a√3 − a Korzystając z funkcji trygonometrycznych:

	FO
tg α =
	IO

	x
√3 =
	y

	x
y =
	√3

	2x
y =
	2√3

	a√3 − a
y =
	2√3

y = U{√3(a√3 − a)}{2√3 * √3)

	3a − a√3
y =
	6

	3a − a√3
2y =
	3

Podstawiając do wzoru na pole rombu:

	2x * 2y		3a − a√3   (a√3 − a)( )   3		a(√3 − 1) * a(3 − √3)
P =		=		=		=
	2		2		2 * 3

	a2(√3 − 1)(3 − √3)		a2(3√3 − 3 − 3 + √3		a2(4√3 − 6)
		=		=		=
	6		6		6

	2a2(2√3 − 3		a2(2√3 − 3)		(2√3 − 3)a2
		=		=
	6		3		3

tim: Oczywiście w miejscu pomyłki kodu powinno być

	√3(a√3 − a)
y =
	2√3 * √3

Ela: dzięki a pozostałe ?