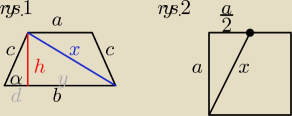pomużcie Justyna: 2) Oblicz miary kąta wewnętrznego, 10−kąta foremnego. 3) Różnica miar kątów przeciwległych trapezu równoramiennego wynosi 30 stopni.Podaj miarę kątów trapezu. 4) W trapezie równoramiennym miara kąta ostrego jest 60 stopni.Wysokość trapezu 3 pierwiastki z 3,a długość przekątnej jest 2 pierwiastki z 19.Podaj obwód trapezu. 5) Wysokośc równoboku spuszczona z wierzchołków kąta rozwartego tworzy z jego ramienia kąt o miarze 72 stopnie.Podaj miary kątów równoległoboku. 6)Podaj długośc boku kwadratu jeśli długośc środka jednego boku od końca przeciwległej na boku jest 3 pierwiastek z 5. zadania podała nam pani więc zadanie 6 nie może być inaczej napisane bo tak nam pani z matematyki podała

Kpt. Sanders: 2) Na chłopski rozum, jest 10 przekątnych, wyobraź sobie okrąg opisany na tym wielokącie, rysujesz te 10 przekątnych. Dzielisz:

360o − miara kąta pełnego (okrąg)
	= 36o
10 − tyle części mamy (w kształcie trójkąta)

Wiadomo, że suma kątów w trójkącie wynosi 180^o. Tak więc: 36^o + α + α = 180^o 180^o − 36^o = 2α 144^o = 2α α = 72^o − to jest kąt przy podstawie trójkąta Kąt wewnętrzny wielokąta to 2α = 144^o 3) Trapez równoramienny ma od góry kąty: α, α, β, β. Kąty naprzeciwległe to kąt lewy górny do prawego dolnego, czyli α−β lub β−α. Przyjmijmy, że β>α, tak więc: β − α =30^o Wiemy również, że suma miar naprzeciwległych kątów wynosi 180^o. Stąd:

⎧	β − α = 30
⎩	α + β = 180

policzyć 4) [rys. 1] α = 60^o h = 3√3 x = 2√19 Mamy trójkąt 30−60−90 o bokach c i h (ten po lewej), z zasady o takim trójkącie wiemy, że c = 2a ← inne a niż na rysunku h = a√3 3√3 = a√3 a = 3 = d c = 2a = 6 Teraz trójkąt o bokach h i x, z zasady Pitagorasa policzymy bok y = b − d: h² + y² = x² y² = x² − h² y = √x² − h² = √(2√19)² − (3√3)² = √76 − 27 = √49 = 7 y = b − d b = y + d = 7 + 3 = 10 a = b − 2d = 10 − 2*3 = 10 − 6 = 4 L = a + b + 2c = ... 5) może jakiś błąd w przepisywaniu, bez dokładnych danych nie pomogę 6) [rys. 2]

	a
a2 + (		)2 = (3√5)2
	2

	a2
a2 +		= 45
	4

5a2
	= 45
4

5a² = 180 a² = 36 a = 6

pigor: ... lub 2) suma kątów 10−cokąta S₁₀= (10−2)*180^o= 8*180^o ⇒ ⇒ α₁₀= ¹₁₀* S{10}= ¹₁₀* 8*180^o= 8*18=144^o . ...

pigor: ..., no to 5) α=90^o−72^o= 18^o , zaś β=90^o+72^o=162^o − szukane miary kątów