?
Patryk: wyznacz największa i najmniejsza wartość funkcji
f(x)=2(3cos2x+1)2−12(3cos2x+1)+16 ,gdzie x∊R
narzuca się 3cos2x+1=t
lecz dalej nie wiem czy porostu obliczyć wsp wierzchołka paraboli , można tak ?
29 lis 18:13
Artur_z_miasta_Neptuna:
jak najbardziej .... pamiętając jednak o tym że t∊<do jakiego przedziału

>
29 lis 18:15
kubkow: t∊<−1;1>
29 lis 18:17
Eta:

29 lis 18:17
Patryk: 3cos2x+1>0 do tego przedziału ?
29 lis 18:17
Ingham: kubkow źle
29 lis 18:18
Patryk: dlaczego t∊<−1;1> ?
29 lis 18:18
Eta:
t€<1,4>

29 lis 18:18
Patryk: why ?
29 lis 18:19
Artur_z_miasta_Neptuna:
a gdzie te −1;1

29 lis 18:19
Ingham: t = 3cos2x + 1, t ∊ ?
czyli t jest zbiorem wartości funkcji 3cos2x + 1
cosx ∊ <−1, 1>
cos2x ∊ <0, 1>
3cos2x ∊ <0, 3>
3cos2x + 1 ∊ <1, 4>
t ∊ <1, 4>
29 lis 18:20
Artur_z_miasta_Neptuna:
gdyby t= cos x
to bym się zgodził
gdyby t=cos
2x to by t∊<0;1>
ale t =
3cos
2x
+1 więc t∊<jakiego

>
29 lis 18:20
kubkow: to była perfidna podpucha !

29 lis 18:22
Eta:
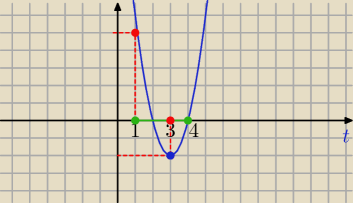
29 lis 18:25
Patryk: max=6
min=−2
nie trzeba wracać do 3cos2x+1 ?
29 lis 18:28
Patryk: ?
29 lis 18:32
Eta:
Tak

( na moim rysunku powinnam wyżej zaznaczyć ( 1,
6)
29 lis 18:36
Patryk: dzieki
29 lis 18:37
 >
>



 >
>


 ( na moim rysunku powinnam wyżej zaznaczyć ( 1, 6)
( na moim rysunku powinnam wyżej zaznaczyć ( 1, 6)