? olka: Rozwiąż nierownosc m² − 16 > 0

olka: sorki m² − 2> 0

Saizou : m²−2>0 (m−√2)(m+√2)>0 dalej dasz radę

O.: skorzystaj z (a−b)(a+b)=a²−b²

kubkow: m² − 2> 0 (m−√2)(m+√2)>0 m∊(−∞;−√2)∪(√2;+∞)

O.: no wlasnie

Saizou : albo m²>2 / √ lml>√2 m>√2 lub m<−√2 zatem m∊(−∞:−√2) U (√2:+∞)

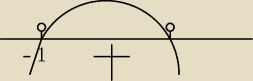
gomol: (m − 1) ( m + 1 ) = 0 m = 1 U m = − 1 m∊ (−1; 1)

olka: a to 5m² − 12> 0

Saizou : 5m²>12

	12
m2>
	5

	2√15
lml>
	5

	2√15		2√15
m>		lub m>−
	5		5

Saizou :

	2√15
znaczy się ten drugi m<−
	5

olka: m² +2 > 0 to wtedy jak?

Patryk: m∊R

olka: dla jakich wartosci parametru m rownanie ma dwa rozne rozwiazania rzeczywiste ujemne: a) x² + mx − m + 3 = 0 b) x² − 2mx + m² − 3m = 0

Ingham: { a ≠ 0 { Δ > 0 { x₁*x₂ < 0 (tutaj wzory Viete'a)

olka: x2 + mx − m + 3 = 0 o to chodzi najbardziej probuje i ciagle wychodza mi glupoty

olka: i jeszcze chyba x1 + x2 < 0 a x1 * x2 to chyba musi byc > 0 bo dwa minusypomnozone daja plus tak mi sie wydaje

olka: no i z delty wychodza mi jakies glupoty