rozwiąż nierówność beataaa: i znów mam prośbę, nawet pare niestety z oporem mi przychodzi przypominanie sobie zadań które miałam na pierwszym roku studiów także mam parę pytań jak to rozwiązać? x³ − 3,5x² + 4,5 >0 b) znaleźć pierwiastki równań * x² + 10x + 9=0 * x³ − 3,5 x² +4,5 = 0 * x³ − 3x² − 9x +17 = 0 dziękuję z góry

Buuu: 2x³ − 7x² + 9 = 2x³ + 2x² − 9x² + 9 = 2x²(x+1) − 9(x² − 1) = 2x²(x+1) − 9(x+1)(x−1) = = (x+1)(2x² − 9x + 9) = ....

beataaa: a skąd to się wzięło? 2x3 − 7x2 + 9 jeśli można to proszę o wytłumaczenie, bo rozwiązane zadanie nic mi nie da, nie zrozumiem tego

Buuu: Równanie zrobiłem razy 2. Teraz z drugiego nawiasu trzeba dlete wyliczyć.

camus: x³−3,5x² + 4,5 > 0 /*2 mnożymy przez 2 2x³ − 7x² + 9 > 0 2x³ +2x² − 9x² +9 > 0 // zauważamy, że 2x² − 9x² = 7x², więc za 7x² podstawiamy lewą strone 2x²(x+1) − 9(x²−1) > 0 //wyciągamy 2x² i −9 przed nawias i zauważamy, że (x²−1) = (x+1)(x−1) − wzór skroconego mnożenia 2x²(x+1) = 9(x+1)(x−1)>0 //co pozwala nam wyciągnąc (x+1) przed nawias (x+1)(2x² −9(x−1)) = (x+1)(2x² − 9x +9) >0 teraz x+1 = 0 , stąd x = −1 2x² −9x +9 = 0 //deltę wyznaczyć i pierwiastki stąd x₁ = ³₂ lub x₂ = 3 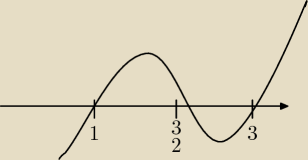Teraz symboliczny rysunek naszej funkcji Ostatecznie, z wykresu wnioskujemy, że funkcja ma wartości większe od 0 w przedziale x∊(1,³₂) ∪ (3,+∞)

beataaa: a to drugie zadanie? znaleźć pierwiastki równań

camus: dokładnie

beataaa: coś takiego będzie? x² + 10x + 9=0 x(x+10)+9=0 ? i co dalej należy zrobić?

Eta: x²+10x+9=0 ⇔ (x+1)(x+9)=0 to x=.... v x=....

beataaa: a gdzie się podziała ta 9 z równania?

krystek: @Eto ? Po maturze?

camus: 10x = 9x + x x² + x + 9x + 9 = x(x+1) + 9(x+1) = (x+1)(x+9)