POle Czworokątów czy ktoś jest w stanie pomóc...: 1. Pole pierścienia wyznaczonego przez okrąg wpisany w kwadrat i okrąg opisany na tym kwadracie jest równe π dm². Oblicz pole kwadratu. 2. W kwadrat o boku długości 6 cm wpisano drugi kwadrat tak, że jego boki tworzą z bokami danego kwadratu kąty odpowiednio 30^o i 60^o. Oblicz pole wpisanego kwadratu. 3. Niech K oznacza kwadrat o boku długości 10 cm, punkt O − jego środek symetrii. Oznaczmy przez K' obraz kwadratu w obrocie dookoła punktu O o kąt 45^o. Oblicz pole figury K∪K' 4. Na bokach kwadratu zbudowano trójkąty równoboczne, których trzecie wierzchołki leżą na zewnątrz danego kwadratu. Wykaż, że łącząc te trzecie wierzchołki odcinkami otrzymamy kwadrat. Oblicz stosunek pól obu kwadratów.

pola: już pomagam

pola: 1. πR²−πr²=π R²−r²=1 R=a√2⇒R²=2a² r=a⇒r²=a² R²−r²=1 2a²−a²=1 a²=1

czy ktoś jest w stanie pomóc...: ale odpowiedz jest 4 dm²

Edek: Zadanie 1. P₀=πR² R=^a√2₂ P_w=πr² r=^a₂ P_o−P_w=π^a2₂−π^a2₄=π^a2₄ P_o−P_w=π π^a2₄=π ^a2₄=1 a²=4 a=2 P_k=a²=4

xD : link do zadania 4 xDD http://matma4u.pl/oblicz-stosunek-pol-kwadratow-t12320.html

Edek: wyobrażmy sobie że tem czworokąt wpisany w ten kwadrat to nasz kwadrat Kąt 30^o zaznacze na niebiesko Kąt 60⁰ na czerwono z własności trójkąta 30^o,60&o,90^o mamy ,czyli x+x√3=6 x(1+√3)=6 x=⁶_1+√3 x=^6*(1−√3_(1+√3)(1−√3) x=^6−6√3₋₂ x=−3+3√3 x=3(√3−1) P_w=(2x)²=(6(√3−1))²=36(3−2√3+1)=144−72√3=72(2−√3)

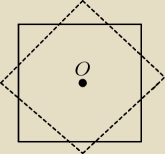
Edek: Zadanie 3.

Edek: jak widzimy trójkąty DBC i EFC są podobne ,czyli SC=10√2−10=10(√2−1)

DB		EF
	=
OC		SC

10√2		EF
	=
5√2		10(√2−1)

EF=20(√2−1) Pole figury = 10² + 4*¹₂*20(√2−1)*10(√2−1)=100+400(√2−1)²=100+400(2−2√2+1)= 100+1200−800√2=1300−800√2=100(13−8√2) Pole figury=100(13−8√2) wytłumaczenie: pole figury to jeden cały kwadrat i cztery małe odstające trójkąciki, obliczyłem ich podstawę i wysokość i wszytsko razem dodałem

Edek: w zadaniu 4 stosunek powinien wynieść 4:1

Ela: ale jak to 4 ? a w tym trzecim to powinno wyjść 200(2−√2).

Ela: prosze..